
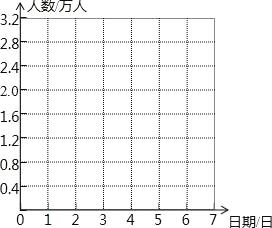
����Ŀ����ʮһ���ƽ����ڼ䣬��������֮���羰����7�������ÿ�����ε������仯���±���������ʾ��ǰһ����������������ʾ��ǰһ���ٵ���������
���� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
�����仯 ��λ������ | +1.6 | +0.8 | +0.4 | ��0.4 | ��0.8 | +0.2 | ��1.2 |
��1�����ж��������ο������������� ���գ����ٵ����� ���գ�
��2����9��30�յ��ο�����Ϊ0�㣬������ͳ��ͼ��ʾ��7����ο������ı仯�����
���𰸡���1��3,7 ��2���𰸼�����
��������
��1������ͳ�Ʊ��ֱ�����ÿ������������������ж�;��2�����ݣ�1���м����ÿ����������Ի�������ͼ��
��1���ɱ�֪1�յ�����Ϊ1.6���ˣ�2������Ϊ2.4���ˣ�3������Ϊ2.8���ˣ�4������Ϊ2.4���ˣ�
5������Ϊ1.6���ˣ�6������Ϊ1.8���ˣ�7������Ϊ0.6���ˣ�
�����������ο�����������3�գ����ٵ�7�գ�
�ʴ�Ϊ��3��7��
��2����9��30�յ��ο�����Ϊ0�㣬������ͳ��ͼ��ʾ��7����ο������ı仯������£�


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1=��2��AC=AD��������һ��������ʹ��ABC�ա�AED�������ӵ�������______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��AD=4��BC=12����E��BC���е㣮��P��Q�ֱ��DZ�AD��BC�ϵ����㣬���е�P��ÿ���1��λ���ȵ��ٶȴӵ�A�˶�����D���ٷ��ص�A��ͬʱ��Q��ÿ��2����λ���ȵ��ٶȴӵ�C�������B�˶���������һ�㵽���յ�ʱֹͣ�˶������˶�ʱ��tΪ_____��ʱ���Ե�A��P��Q��EΪ������ı�����ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ����ǿ��Է�������ijЩ������һ���Ĺ��ɣ���ͼ��2017��12�·ݵ���������ͼ��ѡ��������ĸ������ֱ�ÿ��������Ե�������ˣ�����������磺7��9��1��15= ��18��20��12��26= �����ѷ��֣�������� ��

��1���뽫���������ղ���������
��2�����Ƿ���ѡ���������ƵIJ��ֹ���Ҳ��ͬ������������ʽ����������ϵĹ��ɼ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���֪��A=80�㣬��B=60�㣬DE��BC����ô��CED�Ĵ�С�ǣ������� 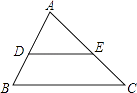
A.40��
B.60��
C.120��
D.140��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ǡ�O��һ�㣬��BAC��ƽ����AD����O�ڵ�D������D��ֱ��AC��ֱ�߽�AC���ӳ����ڵ�E�� 
��1����֤��DE�ǡ�O�����ߣ�
��2����ͼAD=5��AE=4�����O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽ(mx2��2mx��1)(xm��3nx��2)�����Ժ���һ���Ĵζ���ʽ�����Ҳ����������ֱ����m��n��ֵ�������һ����ϵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ�������������ɺ�������⣺
��ͼ����ʾ��AB��CD����˵����B����D����BED.
�⣺����E��EF��CD����֪EF��AB�����ԡ�DEF����D����FEB����B�����ԡ�BED����FEB����DEF����B����D.��ͼ�е�E��λ�÷����仯����ͼ�ڢۢ���ʾ�������������е�������(��С��180��)�к�������ϵ��д�����ۣ���ѡ��ͼ��˵�����ɣ�
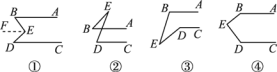
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��CD���ֽ�һֱ��������PMN����ͼ�У����С�P��90�㣬PM��AB�ڵ�E��PN��CD�ڵ�F.
(1)����PMN����λ����ͼ����ʾʱ�������PFD���AEM��������ϵ��
(2)����PMN����λ����ͼ����ʾʱ����֤����PFD����AEM��90�㣻
(3)��(2)�������£���MN��CD���ڵ�O���ҡ�DON��15�㣬��PEB��30�㣬���N�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com