
【题目】已知线段AB,延长AB到C,使BC=![]() AB,D为AC的中点,若BD=6.
AB,D为AC的中点,若BD=6.
(1)画出图形,求AB的长;
(2)若点E在直线AB上,AE=3,求线段ED的长;
(3)若点F在直线AB上,AF=k,求线段FD的长(请直接写出答案、用含k的式子表示).
【答案】(1)16,图形见解析(2)7或13 (3)10+k或10﹣k或k﹣10
【解析】
(1)设BC=x,则AB=4x,依据D为AC中点,可得AD=CD=2.5x,依据BD=6,可得方程2.5x﹣x=6,解得x=4,即可得到AB=16;
(2)如图2,需要分两种情况讨论,(ⅰ)当点E在点A的右边时,(ⅱ)当点E在点A的左边时,根据线段的和差即可得到结论;
(3)如图3,需要分三种情况讨论,(a)当点F在点A的左边时,(b)当点F在点A的右边且在点D的左边时,(c)当点F在点D的右边时,根据线段的和差即可得到结论.
解:(1)如图1,设BC=x,则AB=4x,
∵D为AC中点,
∴AD=CD=2.5x,
∵BD=CD﹣BC=6,
∴2.5x﹣x=6,
解得x=4,
∴AB=16;
(2)如图2,
(ⅰ)当点E在点A的右边时,
由(1)知,AD=2.5x=10,
∵AE=3,
∴DE=AD﹣AE=10-3=7;
(ⅱ)当点E在点A的左边时,
DE=AD+AE=10+3=13;
综上所述,线段ED的长为:7或13;
(3)如图3,
(a)当点F在点A的左边时,DF1=AD+AF1=10+k,
(b)当点F在点A的右边且在D的左边时,DF2=AD﹣AF2=10﹣k,
(c)当点F在点D的右边时,DF3=AF3﹣AD=k﹣10,
综上所述,线段FD的长为:10+k或10﹣k或k﹣10
![]()
![]()


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
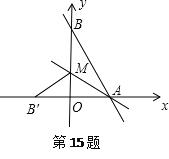
【题目】如图,直线y=﹣![]() x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,求出∠PFD与∠AEM的数量关系;
(2)当△PMN所放位置如图②所示时,求证:∠PFD-∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=15°,∠PEB=30°,求∠N的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
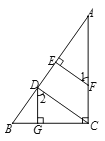
【题目】如图所示,已知:DG⊥BC,AC⊥BC,FE⊥AB,∠1=∠2.
求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直的定义)
∴DG∥AC( )
∴∠2=∠DCA( )
∵∠1=∠2(已知)
∴∠1= (等量代换)
∴ (同位角相等,两直线平行)
∴ =∠ADC( )
∵EF⊥AB(已知), ∴∠AEF=90°( ),∴∠ADC=90° ,
∴CD⊥AB(垂直的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第1次用39万元购进A、B两种商品,销售完后获得利润6万元,它们的进价和售价如下表:(总利润=单件利润×销售量)

(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原价销售,而B商品打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于54000元,则B种商品是打几折销售的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com