
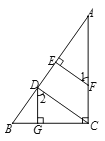
【题目】如图所示,已知:DG⊥BC,AC⊥BC,FE⊥AB,∠1=∠2.
求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直的定义)
∴DG∥AC( )
∴∠2=∠DCA( )
∵∠1=∠2(已知)
∴∠1= (等量代换)
∴ (同位角相等,两直线平行)
∴ =∠ADC( )
∵EF⊥AB(已知), ∴∠AEF=90°( ),∴∠ADC=90° ,
∴CD⊥AB(垂直的定义)
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: ①4a﹣b<0;
②abc<0;
③a+b+c<0;
④a﹣b+c>0;
⑤4a+2b+c>0.
其中错误的个数有( )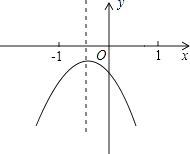
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一台自动测温仪记录的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )

A. 凌晨4时气温最低为-3℃
B. 14时气温最高为8℃
C. 从0时至14时,气温随时间增长而上升
D. 从14时至24时,气温随时间增长而下降
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,延长AB到C,使BC=![]() AB,D为AC的中点,若BD=6.
AB,D为AC的中点,若BD=6.
(1)画出图形,求AB的长;
(2)若点E在直线AB上,AE=3,求线段ED的长;
(3)若点F在直线AB上,AF=k,求线段FD的长(请直接写出答案、用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示﹣ ![]() ,设点B所表示的数为m.
,设点B所表示的数为m. ![]()
(1)求m的值;
(2)求|m﹣1|+(m+6)0的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图,在Rt△ABC中,∠ACB=90°∠BAC=30°.
动手操作:(1)若以直角边AC所在的直线为对称轴.将Rt△ABC作轴对称变换,请你在原图上作出它的对称图形:
观察发现:(2)Rt△ABC和它的对称图形组成了什么图形?你最准确的判断是 .
合作交流:(3)根据上面的图形,请你猜想直角边BC与斜边AB的数量关系,并证明你的猜想.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com