【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论： ①4a﹣b＜0；
②abc＜0；
③a+b+c＜0；
④a﹣b+c＞0；
⑤4a+2b+c＞0．
其中错误的个数有（ ）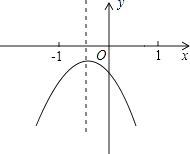
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解：①∵由函数图象开口向下可知，a＜0，由函数的对称轴x=﹣ 
＞﹣2可得b＞4a，故4a﹣b＜0，所以①正确； ②∵a＜0，对称轴在y轴负半轴，则a，b同号，即b＜0，图象与y轴交于负半轴，则c＜0，故abc＜0；所以②正确；
③当x=1时，y=a+b+c＜0，所以③正确；
④当x=﹣1时，y=a﹣b+c＜0，所以④错误；
⑤当x=2时，y=4a+2b+c＜0，所以⑤错误；
故错误的有2个．
故选：B．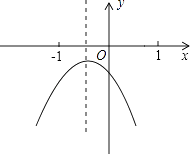
【考点精析】掌握二次函数图象以及系数a、b、c的关系是解答本题的根本，需要知道二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】点 O 是直线 AB上一点，∠COD 是直角，OE平分∠BOC．
（1）①如图1，若∠DOE＝25°，求∠AOC 的度数；
②如图2，若∠DOE＝α，直接写出∠AOC的度数（用含α的式子表示）；
（2）将图 1中的∠COD 绕点O按顺时针方向旋转至图 2 所示位置．探究∠DOE 与∠AOC 的度数之间的关系，写出你的结论，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在日历上，我们可以发现其中某些数满足一定的规律，如图是2017年12月份的日历．如图所选择的两组四个数，分别将每组数中相对的两数相乘，再相减，例如：7×9﹣1×15= ，18×20﹣12×26= ，不难发现，结果都是 ．
（1）请将上面三个空补充完整；
（2）我们发现选择其他类似的部分规律也相同，请你利用整式的运算对以上的规律加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，点C是⊙O上一点，∠BAC的平分线AD交⊙O于点D，过点D垂直于AC的直线交AC的延长线于点E． 
（1）求证：DE是⊙O的切线；
（2）如图AD=5，AE=4，求⊙O的直径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点A的坐标为（3，﹣3），点B的坐标为（﹣1，3），回答下列问题
(1)点C的坐标是 ．
(2)点B关于原点的对称点的坐标是 ．
(3)△ABC的面积为 ．
(4)画出△ABC关于x轴对称的△A′B′C′．
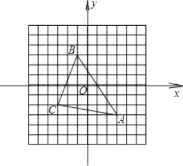
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先阅读所给材料再完成后面的问题：
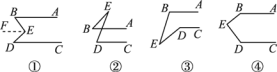
如图①所示，AB∥CD，试说明∠B＋∠D＝∠BED.
解：过点E作EF∥CD，易知EF∥AB，所以∠DEF＝∠D，∠FEB＝∠B，所以∠BED＝∠FEB＋∠DEF＝∠B＋∠D.若图中点E的位置发生变化，如图②③④所示，则上面问题中的三个角(均小于180°)有何数量关系？写出结论，并选择图②说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请根据图中提供的信息,回答下列问题
（1）一个暖瓶与一个水杯分别是多少元?
（2）甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定： 这两种商品都打九折；乙商场规定：买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯，请问选择哪家商场购买更合算，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
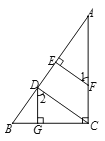
【题目】如图所示，已知：DG⊥BC，AC⊥BC，FE⊥AB，∠1=∠2.
求证：CD⊥AB.
证明：∵DG⊥BC，AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直的定义)
∴DG∥AC( )
∴∠2=∠DCA( )
∵∠1=∠2(已知)
∴∠1= (等量代换)
∴ (同位角相等，两直线平行)
∴ =∠ADC( )
∵EF⊥AB(已知)， ∴∠AEF=90°( )，∴∠ADC=90° ，
∴CD⊥AB(垂直的定义)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com