
【题目】
(1)计算:|﹣ ![]() |+2﹣1+
|+2﹣1+ ![]() (π﹣
(π﹣ ![]() )0﹣tan60°;
)0﹣tan60°;
(2)解分式方程: ![]() .
.
【答案】
(1)
解:原式= ![]() +
+ ![]() +
+ ![]() ×1﹣
×1﹣ ![]() =1
=1
(2)
解:方程的两边同乘(x+1)(x﹣1),得
2(x﹣1)+4=x2﹣1,
即x2﹣2x﹣3=0,
(x﹣3)(x+1)=0,
解得x1=3,x2=﹣1,
检验:把x=3代入(x﹣1)(x+1)=8≠0,即x=3是原分式方程的解,
把x=﹣1代入(x+1)(x﹣1)=0,即x=﹣1不是原分式方程的解,
则原方程的解为:x=3.
【解析】(1)由绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值,即可将原式化简为 ![]() +
+ ![]() +
+ ![]() ×1﹣
×1﹣ ![]() ,继而求得答案;(2)观察可得最简公分母是(x+1)(x﹣1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
,继而求得答案;(2)观察可得最简公分母是(x+1)(x﹣1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
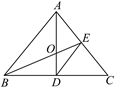
【题目】如图,△ABC的角平分线AD,中线BE相交于点O,有下列结论:①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线.其中正确结论的序号是 ________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,延长AB到C,使BC=![]() AB,D为AC的中点,若BD=6.
AB,D为AC的中点,若BD=6.
(1)画出图形,求AB的长;
(2)若点E在直线AB上,AE=3,求线段ED的长;
(3)若点F在直线AB上,AF=k,求线段FD的长(请直接写出答案、用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A,B两种品牌的龟苓膏粉共1000包.
(1)若小王按需购买A,B两种品牌龟苓膏粉共用22000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式;
(3)在(2)中,小王共用了20000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元,若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本?(运算结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.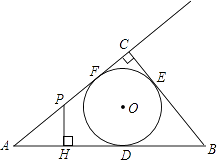
(1)直接写出线段AC、AD及⊙O半径的长;
(2)设PH=x,PC=y,求y关于x的函数关系式;
(3)当PH与⊙O相切时,求相应的y值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面相同的纸牌A、B、C、D其正面分别画有正三角形、圆、平行四边形、正五边形,某同学把这四张牌背面向上洗匀后摸出一张,放回洗匀再摸出一张. 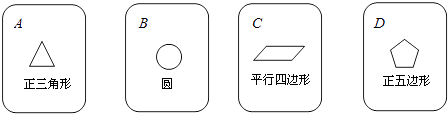
(1)请用树状图或表格表示出摸出的两张牌所有可能的结果;
(2)求摸出两张牌的牌面图形都是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点O(0,0),A(3,0),点B在y轴正半轴上,且△OAB的面积为6,求点B的坐标及直线AB对应的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com