练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．如图a是长方形纸带，∠DEF=26°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是102°．

    分析 先由矩形的性质得出∠BFE=∠DEF=26°，再根据折叠的性质得出∠CFG=180°-2∠BFE，∠CFE=∠CFG-∠EFG即可．

    解答 解：∵四边形ABCD是矩形，
    ∴AD∥BC，
    ∴∠BFE=∠DEF=26°，
    ∴∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°，
    故答案为：102°．

    点评 本题考查了翻折变换（折叠问题）、矩形的性质、平行线的性质；熟练掌握翻折变换和矩形的性质，弄清各个角之间的关系是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

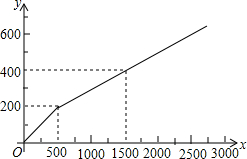    12．为加强与家长的沟通，某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传，该校的印刷任务原来由甲复印店承接，其收费y（元）与印刷页数x（页）的函数关系如图所示．
    （1）从图象中可看出：印刷超过500页部分每页收费0.2元；
    （2）现在乙印刷厂表示：每页0.15元收费．另收200元的制版费，乙印刷厂收费y（元）与印刷页数x（页）的函数关系为y=0.15x+200（x≥0）；
    （3）在给出的坐标系内画出（2）中的函数图象，并结合函数图象回答印刷页数在3000页左右应选择哪个印刷店？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，已知等腰直角三角形ABC的直角边长与正方形DEFG的边长都是4cm，AC与DG在同一直线上，开始时点A与点D重合，△ABC以1cm/s的速度向右移动，最终点A与点G重合，设重合部分（阴影部分）的面积为y（cm2），移动的时间为x（s）．
    （1）求出y与x的函数关系式；
    （2）画出（1）中所写出的函数关系式的图象．
    ①完成下表：
     x/s     
     y/cm2     
    ②画出图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

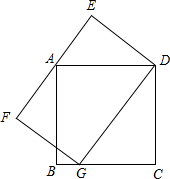    10．已知：如图，正方形的顶点A在矩形DEFG的边EF上，矩形DEFG的顶点G在正方形的边BC上，正方形的边长为4，DG的长为6，则DE的长为$\frac{8}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

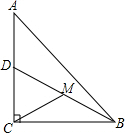    17．如图，在Rt△ABC中，∠ACB=90°，D为AC的中点，M为BD的中点，将线段AD绕A点任意旋转（旋转过程中始终保持点M为BD的中点），若AC=4，BC=3，那么在旋转过程中，线段CM长度的取值范围是1.5≤CM≤3.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

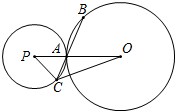    7．如图，已知⊙O的半径为5，⊙P与⊙O外切于点A，经过点A的直线与⊙O、⊙P分别交于点B、C，tan∠OAB=$\frac{\sqrt{21}}{2}$．
    （1）求AB的长；
    （2）当∠OCA=∠OPC时，求⊙P的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

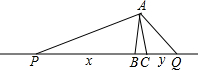    14．如图，在△ABC中，AB=AC，∠BAC=20°，P，Q在直线BC上，且∠PAQ=100°．设BP=x，CQ=y，则下列结论正确的是（　　）
    A．当x≠y时，△APB≌△AQCB．当x=y时，∠APB=∠PAB=45°
    C．当x=2y时，$\frac{AP}{AQ}$=$\sqrt{2}$D．当x•y=4时，AB=4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．x为何值时，分式$\frac{x}{x-1}$的值比$\frac{2}{x+1}$的值多1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

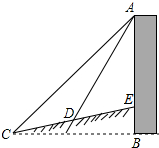    12．重庆建筑多因地制宜、依山而建，现有以住宅楼如图所示，该楼背后为一斜坡，坡角为15°，为测得该楼的高度，一兴趣小组的同学在C点测得楼顶A点的仰角为45°，点D点测的仰角为60°，CD两点之间的距离是20米，C、B在同一水平地面上，CD与AB交于点E．
    （1）求D点距离地面的垂直距离；
    （2）求斜坡最高点E点到楼顶A点之间的距离．
    （结果保留根号，参考数据：tan15°=0.27，sin15°=0.26，cos15°=0.97，$\sqrt{3}$=1.732，$\sqrt{2}$=1.414，$\sqrt{6}$=2.449）

    查看答案和解析>>

    同步练习册答案