
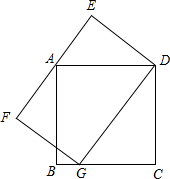
 已知:如图,正方形的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形的边BC上,正方形的边长为4,DG的长为6,则DE的长为$\frac{8}{3}$.
已知:如图,正方形的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形的边BC上,正方形的边长为4,DG的长为6,则DE的长为$\frac{8}{3}$. 分析 首先根据矩形和正方形的性质可得,∠EDC=∠ADC=90°,∠E=∠C=90°,可判断△AED∽△GCD,然后根据相似三角形的性质得出$\frac{DE}{AD}$=$\frac{CD}{DG}$,代入数据即可求出DE的长度.
解答 解:在正方形ABCD和矩形DEFG中,
∵∠EDC=∠ADC=90°,∠E=∠C=90°,
∴∠EAD+∠ADG=∠ADG+∠GCD=90°,
∴∠EAD=∠GCD,
∴△AED∽△GCD,
则有$\frac{DE}{AD}$=$\frac{CD}{DG}$,
∵AD=CD=4,DG=6,
∴ED=$\frac{AD•CD}{DG}$=$\frac{4×4}{6}$=$\frac{8}{3}$.
故答案为:$\frac{8}{3}$.
点评 本题考查了相似三角形的判定和性质,涉及了正方形和矩形的性质,解答本题的关键是根据题意判定得出∠EAD=∠GCD,进而证明△AED∽△GCD.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:选择题
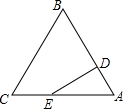 如图,边长为3的等边△ABC中,D为AB的三等分点(AD=$\frac{1}{2}$BD),三角形边上的动点E从点A出发,沿A→C→B的方向运动,到达点B时停止,设点E运动的路程为x,DE2=y,则y关于x的函数图象大致为( )
如图,边长为3的等边△ABC中,D为AB的三等分点(AD=$\frac{1}{2}$BD),三角形边上的动点E从点A出发,沿A→C→B的方向运动,到达点B时停止,设点E运动的路程为x,DE2=y,则y关于x的函数图象大致为( )| A. | 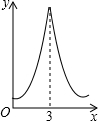 | B. | 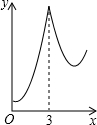 | C. | 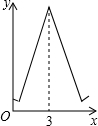 | D. | 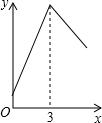 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
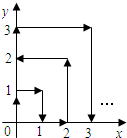 一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动【即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,1)…】,且每秒移动一个单位,那么第41秒时质点所在位置的坐标是(6,5).
一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动【即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,1)…】,且每秒移动一个单位,那么第41秒时质点所在位置的坐标是(6,5).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,-4) | B. | (2,-3) | C. | (-3,2) | D. | (4,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
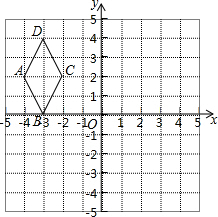 下面方格中有一个菱形ABCD和点O,请你在方格中画出以下图形(只要求画出平移、旋转后的图形,不要求写出作图步骤和过程).
下面方格中有一个菱形ABCD和点O,请你在方格中画出以下图形(只要求画出平移、旋转后的图形,不要求写出作图步骤和过程).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
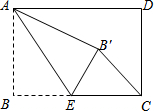 如图,长方形的宽AB=3,长BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.
如图,长方形的宽AB=3,长BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
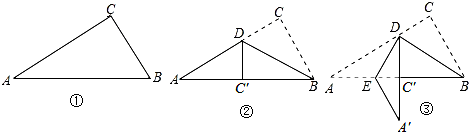
| A. | $2\sqrt{2}$cm | B. | $2\sqrt{3}$cm | C. | $\frac{8}{3}$cm | D. | 3cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com