
| A. | (3,-4) | B. | (2,-3) | C. | (-3,2) | D. | (4,-3) |
分析 先画出图形,证△AMB≌△A′NB,推出AM=A′N,MB=NB,即可求出对称点的坐标.
解答 解: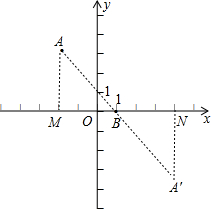
如图,设A关于B的对称点是A′,过A作AM⊥x轴于M,过A′作A′N⊥x轴于N,
则∠AMO=∠A′NO=90°,
∵在△AMB和△A′NB中
$\left\{\begin{array}{l}{∠AOM=∠A′ON}\\{∠AMO=∠A′NO}\\{AB=A′B}\end{array}\right.$
∴△AMB≌△A′NB,
∴AM=A′N,MB=NB,
∵点A(-2,3)、点B(1,0),
∴A′N=AM=3,MB=NB=3,ON=1+3=4,
∴A′的坐标是(4,-3),
故选D.
点评 本题考查了坐标与图形性质,全等三角形的性质,对称点的性质的应用,解此题的关键是能正确画出图形,难度适中.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
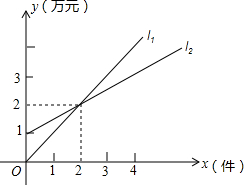 如图,l1表示某个公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.
如图,l1表示某个公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
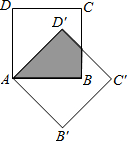 如图,边长为2的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是4$\sqrt{2}$-4.
如图,边长为2的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是4$\sqrt{2}$-4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知等腰直角三角形ABC的直角边长与正方形DEFG的边长都是4cm,AC与DG在同一直线上,开始时点A与点D重合,△ABC以1cm/s的速度向右移动,最终点A与点G重合,设重合部分(阴影部分)的面积为y(cm2),移动的时间为x(s).
如图,已知等腰直角三角形ABC的直角边长与正方形DEFG的边长都是4cm,AC与DG在同一直线上,开始时点A与点D重合,△ABC以1cm/s的速度向右移动,最终点A与点G重合,设重合部分(阴影部分)的面积为y(cm2),移动的时间为x(s).| x/s | |||||
| y/cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
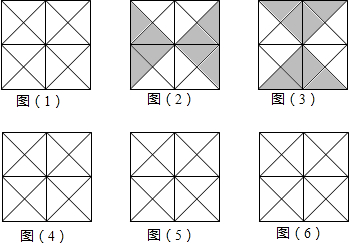
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
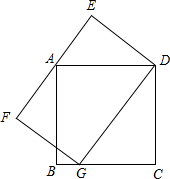 已知:如图,正方形的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形的边BC上,正方形的边长为4,DG的长为6,则DE的长为$\frac{8}{3}$.
已知:如图,正方形的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形的边BC上,正方形的边长为4,DG的长为6,则DE的长为$\frac{8}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
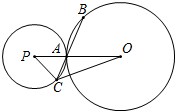 如图,已知⊙O的半径为5,⊙P与⊙O外切于点A,经过点A的直线与⊙O、⊙P分别交于点B、C,tan∠OAB=$\frac{\sqrt{21}}{2}$.
如图,已知⊙O的半径为5,⊙P与⊙O外切于点A,经过点A的直线与⊙O、⊙P分别交于点B、C,tan∠OAB=$\frac{\sqrt{21}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com