
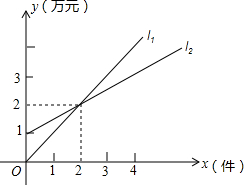
 如图,l1表示某个公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.
如图,l1表示某个公司一种产品一天的销售收入与销售量的关系,l2表示该公司这种产品一天的销售成本与销售量的关系.分析 (1)根据线段中点的求法列式计算即可求出x=1时的销售收入和销售成本,根据盈利的求法计算即可得解;
(2)设l2对应的函数表达式为l2=kx+b(k≠0),l1对应的函数表达式为:l1=ax,然后利用待定系数法求一次函数解析式解答;
(3)根据利润=销售收入-销售成本列式整理,进而求出即可.
解答 解:(1)x=2时,销售收入2万元,销售成本2万元,盈利(收入-成本)=2-2=0(万元);
故答案为:2,2,0;
(2)设l2对应的函数表达式为l2=kx+b(k≠0),
∵函数图象经过点(0,1),(2,2),
∴$\left\{\begin{array}{l}{b=1}\\{2k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴l2对应的函数表达式是l2=$\frac{1}{2}$x+1,
设l1对应的函数表达式为:l1=ax,则2=2a,解得:a=1,
故l1对应的函数表达式为:l1=x;
(3)∵利润=l1-l2=x-($\frac{1}{2}$x+1)=$\frac{1}{2}$x-1,
∴当6=$\frac{1}{2}$x-1,
解得:x=14,
故当销售量是14件时,利润为6万元.
点评 本题考查了一次函数的应用,考查了识别函数图象的能力,待定系数法求一次函数解析式,准确观察图象提供的信息是解题的关键.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
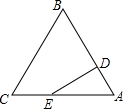 如图,边长为3的等边△ABC中,D为AB的三等分点(AD=$\frac{1}{2}$BD),三角形边上的动点E从点A出发,沿A→C→B的方向运动,到达点B时停止,设点E运动的路程为x,DE2=y,则y关于x的函数图象大致为( )
如图,边长为3的等边△ABC中,D为AB的三等分点(AD=$\frac{1}{2}$BD),三角形边上的动点E从点A出发,沿A→C→B的方向运动,到达点B时停止,设点E运动的路程为x,DE2=y,则y关于x的函数图象大致为( )| A. |  | B. |  | C. | 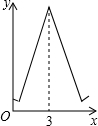 | D. | 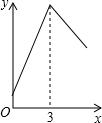 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
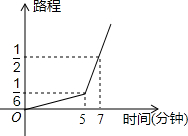 一名考生步行前往考场,5分钟走了总路程的$\frac{1}{6}$,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示,则他到达考场所花的时间比一直步行提前了20分钟.
一名考生步行前往考场,5分钟走了总路程的$\frac{1}{6}$,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示,则他到达考场所花的时间比一直步行提前了20分钟.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
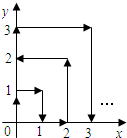 一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动【即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,1)…】,且每秒移动一个单位,那么第41秒时质点所在位置的坐标是(6,5).
一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动【即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→(2,1)…】,且每秒移动一个单位,那么第41秒时质点所在位置的坐标是(6,5).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,-4) | B. | (2,-3) | C. | (-3,2) | D. | (4,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
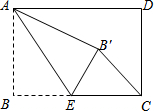 如图,长方形的宽AB=3,长BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.
如图,长方形的宽AB=3,长BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com