练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

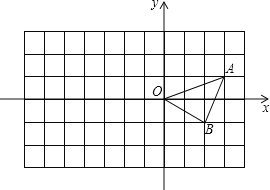
    【题目】如图，已知O是坐标原点，A、B的坐标分别为（3，1）、（2，﹣1）．

    （1）在y轴的左侧以O为位似中心作△OAB的位似三角形OCD，使新图与原图的相似比为2：1；

    （2）分别写出A，B的对应点C、D的坐标；

    （3）求△OCD的面积．

    【答案】（1）详见解析；（2）C（﹣6，﹣2），D（﹣4，2）；（3）10．

    【解析】

    （1）延长AO到C使得OC＝2OA，延长BO到D，使得OD＝2OB，连接CD，△OCD即为所求；

    （2）根据C，D的位置写出坐标即可；

    （3）利用分割法求出三角形的面积即可．

    解：（1）如图，△OCD即为所求．

    （2）由图可得：C（﹣6，﹣2），D（﹣4，2），

    （3）S△OCD＝24﹣×4×2﹣×6×2﹣×2×4＝10．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：在△ABC 中，AB=AC.

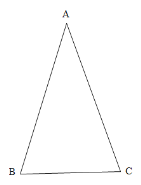
    （1）求作△ABC 外接圆（尺规作图）

    （2）若△ABC 的外接圆的圆心O到 BC 边的距离为 4，BC=6,求外接圆的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】材料一：一个正整数x能写成x=a2﹣b2（a，b均为正整数，且a≠b），则称x为“雪松数”，a，b为x的一个平方差分解，在x的所有平方差分解中，若a2+b2最大，则称a，b为x的最佳平方差分解，此时F（x）=a2+b2．

    例如：24=72﹣52，24为雪松数，7和5为24的一个平方差分解，32=92﹣72，32=62﹣22，因为92+72＞62+22，所以9和7为32的最佳平方差分解，F（32）=92+72

    材料二：若一个四位正整数，它的千位数字与个位数字相同，百位数字与十位数字相同，但四个数字不全相同，则称这个四位数为“南麓数”．例如4334，5665均为“南麓数”．

    根据材料回答：

    （1）请直接写出两个雪松数，并分别写出它们的一对平方差分解；

    （2）试证明10不是雪松数；

    （3）若一个数t既是“雪松数”又是“南麓数”，并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解，请求出所有满足条件的数t中F（t）的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

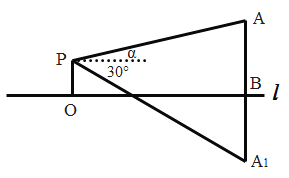
    【题目】在湖心有一座小塔，小华想知道这座的高塔的高度，于是他在岸边架起了测角仪，他测量的数据如下（如图所示）：测量仪位置距水平面的距离为1.5米（即），测得塔顶的仰角为（其中），测得塔顶在水中倒影（即）的俯角为，请你根据上述数据求出这座塔的高度（即）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，E是边CD上一点（点E不与点C、D重合），连结BE．

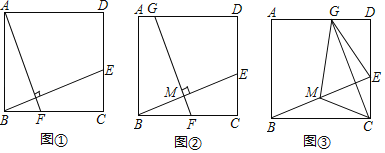
    （感知）如图①，过点A作AF⊥BE交BC于点F．易证△ABF≌△BCE．（不需要证明）

    （探究）如图②，取BE的中点M，过点M作FG⊥BE交BC于点F，交AD于点G．

    （1）求证：BE=FG．

    （2）连结CM，若CM=1，则FG的长为　 　．

    （应用）如图③，取BE的中点M，连结CM．过点C作CG⊥BE交AD于点G，连结EG、MG．若CM=3，则四边形GMCE的面积为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

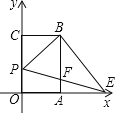
    【题目】如图，已知矩形OABC，以点O为坐标原点建立平面直角坐标系，其中A（2，0），C（0，3），点P以每秒1个单位的速度从点C出发在射线CO上运动，连接BP，作BE⊥PB交x轴于点E，连接PE交AB于点F，设运动时间为t秒．

    （1）当t＝4时，求点E的坐标；

    （2）在运动的过程中，是否存在以P、O、E为顶点的三角形与△ABE相似．若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

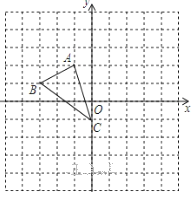
    【题目】如图，在平面直角坐标系网格中，△ABC的顶点都在格点上，点C坐标(0，-1)．

    作出△ABC 关于原点对称的△A1B1C1，并写出点A1的坐标；

    把△ABC 绕点C逆时针旋转90°，得△A2B2C2，画出△A2B2C2，并写出点A2的坐标；

    (3)直接写出△A2B2C2的面积

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，D、E为⊙O上位于AB异侧的两点，连接BD并延长至点C，使得CD=BD，连接AC交⊙O于点F，连接AE、DE、DF．

    （1）证明：∠E=∠C；

    （2）若∠E=55°，求∠BDF的度数；

    （3）设DE交AB于点G，若DF=4，cosB=，E是弧AB的中点，求EGED的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

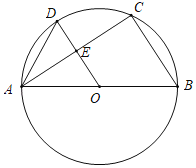
    【题目】如图，AB是⊙O的直径，C、D是⊙O上的两点，且OD∥BC，OD与AC交于点E，连接AD．

    （1）求证：AE＝CE；

    （2）若∠B＝60°，求∠CAD的度数；

    （3）若AC＝4，BC＝3，求DE的长．

    查看答案和解析>>

    同步练习册答案