
分析 (1)先利用因式分解法求出方程x2-mx+m=x的根为x=m或1,再把x=m代入x2+mx-4=0,求得m=±$\sqrt{2}$;把x=1代入x2+mx-4=0,求得m=3;
(2)先由(1)可得m=-$\sqrt{2}$,再解方程x2-$\sqrt{2}$x-4=0,求出x=2$\sqrt{2}$或-$\sqrt{2}$,再分别代入$\frac{3}{s}$+$\frac{3}{2-s}$=$\frac{3(2-s)+3s}{s(2-s)}$=$\frac{6}{2s-{s}^{2}}$,计算即可求解.
解答 解:(1)∵x2-mx+m=x,
∴x2-(m+1)x+m=0,
∴(x-m)(x-1)=0,
∴x=m或1.
把x=m代入x2+mx-4=0,得m2+m•m-4=0,
解得m=±$\sqrt{2}$;
把x=1代入x2+mx-4=0,得12+m•1-4=0,
解得m=3.
故满足要求的所有m的值为±$\sqrt{2}$或3;
(2)由题意可得m=-$\sqrt{2}$,
解方程x2-$\sqrt{2}$x-4=0,
解得x=$\frac{\sqrt{2}±\sqrt{18}}{2}$,
x=2$\sqrt{2}$或-$\sqrt{2}$.
$\frac{3}{s}$+$\frac{3}{2-s}$=$\frac{3(2-s)+3s}{s(2-s)}$=$\frac{6}{2s-{s}^{2}}$,
当s=2$\sqrt{2}$时,原式=$\frac{6}{4\sqrt{2}-8}$=-$\frac{3\sqrt{2}+6}{4}$;
当s=-$\sqrt{2}$时,原式=$\frac{6}{-2\sqrt{2}-2}$=-3$\sqrt{2}$+3.
点评 本题考查了一元二次方程的解的意义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了一元二次方程的解法,正确求出方程x2-mx+m=x的根是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
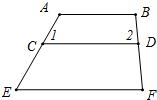 如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论.
如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com