【题目】在下列命题中：①有一个外角是
的等腰三角形是等边三角形；②有两个外角相等的等腰三角形是等边三角形；③有一边上的高也是这边上的中线的三角形是等边三角形；④三个外角都相等的三角形是等边三角形．正确的命题有（ ）
A.4个B.3个C.2个D.1个
【答案】C
【解析】
根据等边三角形的性质和定义可得：有一个角为60°的等腰三角形为等边三角形；三个内角相等的三角形为等边三角形；再根据中线的性质和三角形内角和的定义进一步分析即可.
有一个外角是
的等腰三角形，即其有一个内角为60°，而有一个角为60°的等腰三角形是等边三角形，故①正确；
两个外角相等说明该三角形中有两个内角相等，而等腰三角形的两个内角就是相等的，故该条件无法确定该三角形是等边三角形，故②错误；
等腰三角形的底边上的高也是该边上的中线，故该条件无法确定该三角形为等边三角形，故③错误；
三个外角都相等，则说明三个内角也都相等，即该三角形为等边三角形，故④正确；
综上所述，一共两个正确，
故选：C.
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°，AE是△ABC的角平分线；ED平分∠AEB交AB于点D；∠CAE=∠B．
（1）如果AC=3.5 cm，求AB的长度；
（2）猜想：ED与AB的位置关系，并证明你的猜想。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
的三个顶点在边长为1的正方形网格中，已知
，
，
.
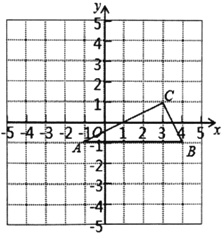
(1)画出关于
轴对称的
(其中
，
，
分别是
，
，
的对应点，不写画法)；
(2)分别写出，，三点的坐标.
(3)请写出所有以
为边且与全等的三角形的第三个顶点(不与重合)的坐标_____.
查看答案和解析>>
科目：初中数学 来源： 题型：
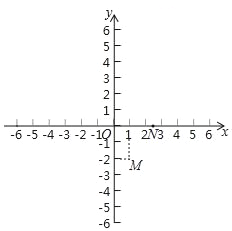
【题目】已知抛物线y=ax2+bx+c（x为任意实数）经过下图中两点M（1，﹣2）、N（m，0），其中M为抛物线的顶点，N为定点．下列结论：
①若方程ax2+bx+c=0的两根为x1，x2（x1＜x2），则﹣1＜x1＜0，2＜x2＜3；
②当x＜m时，函数值y随自变量x的减小而减小．
③a＞0，b＜0，c＞0．
④垂直于y轴的直线与抛物线交于C、D两点，其C、D两点的横坐标分别为s、，则s+t=2．
其中正确的是（ ）
A. ①② B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是“经过圆外一点作圆的切线”的尺规作图的过程．
已知：P为外一点．求作：经过P点的切线．作法：如图，（1）连结OP；（2）以OP为直径作圆，与交于C、D两点．（3）作直线PC、PD．则直线PC、PD就是所求作经过P点的切线．以上作图的依据是：_____．
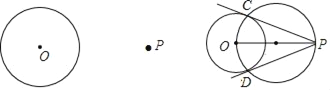
查看答案和解析>>
科目：初中数学 来源： 题型：
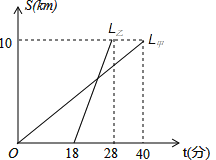
【题目】如图，甲乙两人以相同的路线前往距离单位
的培训中心参加学习，图中
，
分别表示甲乙两人前往目的地所走的路程
(千米)随时间
(分)变化的函数图象，以下说法：
①乙比甲提前12分钟到达
②甲平均速度为0.25千米/小时
③甲、乙相遇时，乙走了6千米
④乙出发6分钟后追上甲，其中正确的是( )
A.①②B.③④C.①③④D.②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
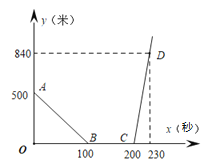
【题目】小明和妈妈开车去中央公园采风，小明爸爸发现他们忘记带画笔后立即开车追赶他们.假设妈妈和爸爸的车在同一直线公路上匀速行驶，当爸爸的车追上妈妈的车后，两车停下来，爸爸把画笔交给小明.然后小明和妈妈开车以原来速度的
倍继续前行，爸爸则以来时一半的速度沿原路回家．设小明爸爸开车的时间为
（秒），两车间的距离为
（米），关于的部分函数关系如图所示，当小明爸爸回到家时，小明和妈妈正好行驶了全程的
，则小明家离中央公园的距离为________米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数
的图象经过点
，点
，交y轴于点C，给出下列结论：
：b：
：2：3；
若
，则
；
对于任意实数m，一定有
；
一元二次方程
的两根为
和
，其中正确的结论是
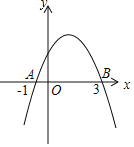
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
