
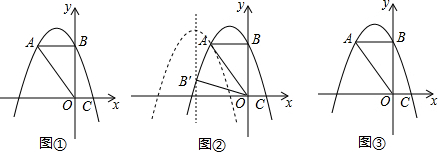
���� ��1����ͼ�٣�����AB��y��õ�B��0��3����Ȼ���B��������������߽���ʽ�����c��ֵ��
��2����ͼ�ڣ���B�䣨a��b���������۵������ʵ�AB��=AB=2��OB��=OB=3�����������ľ��빫ʽ�õ�$\left\{\begin{array}{l}{��a+2��^{2}+��b-3��^{2}={2}^{2}}\\{{a}^{2}+{b}^{2}={3}^{2}}\end{array}\right.$����ⷽ����ɵõ�B�䣨-$\frac{36}{13}$��$\frac{15}{13}$�������ǿ�ȷ��P��
��3����ͼ�ۣ���ȷ��C��1��0��������BCֻ��Ϊ�ߣ�����Ϊ�Խ��ߣ���Ӧ��EF��BC��EF=BC�ɵõ�F���������Ϊ3��-3����y=3ʱ��-x2-2x+3=3���ⷽ��ȷ����ʱF�������Ϊ��-2��3��������ƽ���ı��ε����ʿɵõ���ӦE������Ϊ��-1��0������y=-3ʱ��-x2-2x+3=-3����÷��̵õ�F�������Ϊ��-1+$\sqrt{7}$��-3����-1-$\sqrt{7}$��-3��������ƽ���ı��ε����ʿ�ȷ����Ӧ��E������꣨-2+$\sqrt{7}$��0����-2-$\sqrt{7}$��0����
��� �⣺��1����ͼ�٣�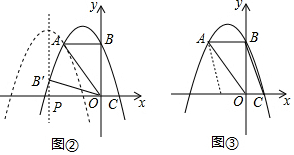
�ߵ�A�������ǣ�-2��3������A��AB��y�ᣬ
��B��0��3����
��B��0��3������y=-x2-2x+c��c=3��
��2����ͼ�ڣ���B�䣨a��b����
�ߡ�OAB��ֱ��OA���ۣ��ǵ�B�Ķ�Ӧ��ΪB�䣬
��AB��=AB=2��OB��=OB=3��
��$\left\{\begin{array}{l}{��a+2��^{2}+��b-3��^{2}={2}^{2}}\\{{a}^{2}+{b}^{2}={3}^{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{a=0}\\{b=3}\end{array}\right.$��$\left\{\begin{array}{l}{a=-\frac{36}{13}}\\{b=\frac{15}{13}}\end{array}\right.$��
��B�䣨-$\frac{36}{13}$��$\frac{15}{13}$����
�ߵ�B'ǡ������ƽ�ƺ������ߵĶԳ����ϣ�
��P��-$\frac{36}{13}$��0����
��3����ͼ�ۣ������߽���ʽΪy=-x2-2x+3����y=0ʱ��-x2-2x+3=0�����x1=1��x2=-3����C��1��0����
�Ե�B��C��E��FΪ������ı�����ƽ���ı��Σ���BCΪ�ߣ�����Ϊ�Խ��ߣ�
��EF��BC��EF=BC��
��F���������Ϊ3��-3��
��y=3ʱ��-x2-2x+3=3�����x1=0��x2=-2����ʱF�������Ϊ��-2��3��������E������Ϊ��-1��0����
��y=-3ʱ��-x2-2x+3=-3�����x1=-1+$\sqrt{7}$��x2=-1-$\sqrt{7}$��
��ʱF�������Ϊ��-1+$\sqrt{7}$��-3����-1-$\sqrt{7}$��-3������Ӧ��E������꣨-2+$\sqrt{7}$��0����-2-$\sqrt{7}$��0����
����������E���������-1��0������-2+$\sqrt{7}$��0����-2-$\sqrt{7}$��0����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ���������������κ��������ʡ��۵������ʺ�ƽ���ı��ε����ʣ������ô���ϵ�����������ߵĽ���ʽ�������������ľ��빫ʽ�����߶εij�����Ӧ�÷������۵�˼������ѧ���⣮


 Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
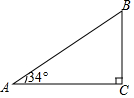 ��ͼ��ijɽ���³�ABΪ110�ף��½ǣ���A��Ϊ34�㣬���¸�BC���¿�AC���������ȷ��0.1�ף�
��ͼ��ijɽ���³�ABΪ110�ף��½ǣ���A��Ϊ34�㣬���¸�BC���¿�AC���������ȷ��0.1�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -2 | C�� | $\frac{1}{3}$ | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
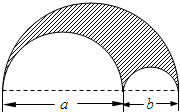 ��ͼ��һ��ֱ��Ϊa+b�İ�Բ�θְ壬������ȥֱ���ֱ�Ϊa��b��������Բ
��ͼ��һ��ֱ��Ϊa+b�İ�Բ�θְ壬������ȥֱ���ֱ�Ϊa��b��������Բ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
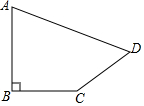 ��ͼ��ʾ�����ı���ABCD�У���B=90�㣬AB=2��BC=CD=1��AD=$\sqrt{6}$�������ı���ABCD�������
��ͼ��ʾ�����ı���ABCD�У���B=90�㣬AB=2��BC=CD=1��AD=$\sqrt{6}$�������ı���ABCD��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com