
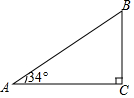
 如图,某山坡坡长AB为110米,坡角(∠A)为34°,求坡高BC及坡宽AC.(结果精确到0.1米)
如图,某山坡坡长AB为110米,坡角(∠A)为34°,求坡高BC及坡宽AC.(结果精确到0.1米) 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
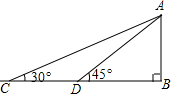 如图,某数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端点A的仰角为30°,再向旗杆的方向前进12米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端点A的仰角为45°,请计算旗杆AB的高度.(结果保留根号)
如图,某数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端点A的仰角为30°,再向旗杆的方向前进12米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端点A的仰角为45°,请计算旗杆AB的高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
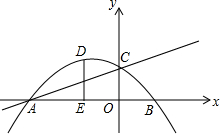 如图,抛物线y=ax2+bx+1与直线y=-ax+c相交于坐标轴上点A(-3,0),C(0,1)两点.
如图,抛物线y=ax2+bx+1与直线y=-ax+c相交于坐标轴上点A(-3,0),C(0,1)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
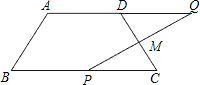 如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.
如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
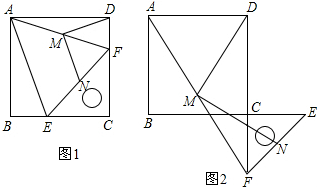
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
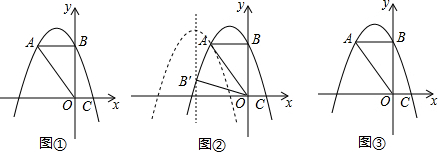
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com