练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．下列四个图形中，既是轴对称图形又是中心对称图形的是（　　）
    A．
    等边三角形    		B．
    平行四边形    		C．
    正六边形    		D．
    五角星

    分析 根据轴对称图形与中心对称图形的概念求解．

    解答 解：A、是轴对称图形．不是中心对称图形，因为找不到任何这样的一点，旋转180度后它的两部分能够重合；即不满足中心对称图形的定义．故此选项不合题意；
    B、不是轴对称图形，因为找不到任何这样的一条直线，沿这条直线对折后它的两部分能够重合；即不满足轴对称图形的定义．是中心对称图形．故此选项不合题意；
    C、是轴对称图形，又是中心对称图形．故此选项符合题意；
    D、是轴对称图形．不是中心对称图形，因为找不到任何这样的一点，旋转180度后它的两部分能够重合；即不满足中心对称图形的定义．故此选项不合题意．
    故选：C．

    点评 此题主要考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后两部分重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

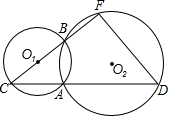    20．如图，已知⊙O1与⊙O2交于A，B两点，点C在⊙O1上且在⊙O2外，CA，CB的延长线分别与⊙O2交于点D，E，AC=3，AD=6，⊙O1的半径为2．则点O1到DE的距离为 （　　）
    A．$\frac{17}{4}$B．$\frac{9}{2}$C．$\frac{19}{4}$D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．解方程：
    （1）（4x-1）2-9=0
    （2）3（x-2）2=2-x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

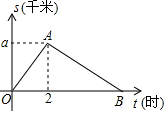    18．某单位举行“健康人生”徒步走活动，某人从起点体育村沿建设路到市生态园，再沿原路返回，设此人离开起点的路程s（千米）与走步时间t（小时）之间的函数关系如图所示，其中从起点到市生态园的平均速度是4千米/小时，用2小时，根据图象提供信息，解答下列问题．
    （1）求图中的a值．
    （2）若在距离起点5千米处有一个地点C，此人从第一次经过点C到第二次经过点C，所用时间为1.75小时．
    ①求AB所在直线的函数解析式；
    ②请你直接回答，此人走完全程所用的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

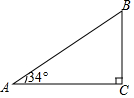    5．如图，某山坡坡长AB为110米，坡角（∠A）为34°，求坡高BC及坡宽AC．（结果精确到0.1米）
    【参考数据：sin34°=0.559，cos34°=0.829，tan34°=0.675】

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．若a2+a=0，则2a2+2a+2016的值为2016．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

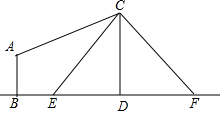    2．如图，电线杆CD上的C处引拉线CE，CF固定电线杆，在离电线杆6米的B处安置测角仪（点B，E，D在同一直线上），在A处测得电线杆上C处的仰角为30°，已知测角仪的高AB=$\sqrt{3}$米，BE=3米，求拉线CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．完成下列解题过程．
    如图．己知CD垂直于AB，FG垂直于AB，∠1=∠2，求证：DE∥BC．
    解：因为CD⊥AB，FG⊥FG（已知）
    所以∠CDB=∠FGB=90°，
    所以CD∥GF（两直线平行，同位角相等）．
    又因为∠1=∠2（已知），
    所以∠2=∠DCB（等量代换）
    所以DE∥BC（同位角相等，两直线平行）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，正比例函数y=ax与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点M（$\sqrt{6}$，$\sqrt{6}$）．
    （1）求这两个函数的表达式；
    （2）如图1，若∠AMB=90°，且其两边分别于两坐标轴的正半轴交于点A、B．求四边形OAMB的面积．
    （3）如图2，点P是反比例函数y=$\frac{k}{x}$（x＞0）的图象上一点，过点P作x轴、y轴的垂线，垂足分别为E、F，PF交直线OM于点H，过作x轴的垂线，垂足为G．设点P的横坐标为m，当m＞$\sqrt{6}$时，是否存在点P，使得四边形PEGH为正方形？若存在，求出P点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案