
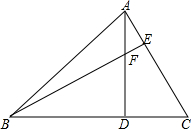
 如图,BF=AC,FD=CD,BD=AD,求证:AC⊥BE.
如图,BF=AC,FD=CD,BD=AD,求证:AC⊥BE. 分析 首先证明△BDF≌△ADC,则∠ADB=∠ADC,∠DBF=∠DAC,据此即可证明∠ADB=∠ADC=90°,然后利用三角形的内角和定理即可证得∠AEF=90°,进而证明垂直.
解答 证明:∵△BDF和△ADC中,
$\left\{\begin{array}{l}{BF=AC}\\{FD=CD}\\{BD=AD}\end{array}\right.$,
∴△BDF≌△ADC,
∴∠ADB=∠ADC,∠DBF=∠DAC,
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴∠DBF+∠BFD=90°,
又∵∠AFE=∠BFD,∠DBF=∠DAC,
∴∠DAC+∠AFE=90°,
∴∠AEF=90°,
∴AC⊥BE.
点评 本题考查了三角形全等的判定与性质以及三角形内角和定理,证明∠ADB=∠ADC=90°是本题的关键.


科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:单选题
把一元二次方程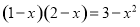 化成一般形式
化成一般形式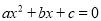 (a≠0),其中a、b、c 的值分别为( )
(a≠0),其中a、b、c 的值分别为( )
A. 2、3、﹣1 B. 2、﹣3、1 C. 2、﹣3、﹣1 D. 2、3、1
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com