
分析 (1)根据配方法的一般步骤:把常数项移到等号的右边;把二次项的系数化为1;等式两边同时加上一次项系数一半的平方,可得答案;
(2)根据配方法的一般步骤:把常数项移到等号的右边;把二次项的系数化为1;等式两边同时加上一次项系数一半的平方,可得答案;
(3)根据配方法的一般步骤:把常数项移到等号的右边;把二次项的系数化为1;等式两边同时加上一次项系数一半的平方,可得答案;
(4)根据配方法的一般步骤:把常数项移到等号的右边;把二次项的系数化为1;等式两边同时加上一次项系数一半的平方,可得答案.
解答 解:(1)移项,得
x2+8x=2,
配方,得
(x+4)2=18,
开方,得
x+4=±3$\sqrt{2}$,
x1=-4+3$\sqrt{2}$,x2=-4-3$\sqrt{2}$;
(2)移项,得
x2-x=1,
配方,得
(x-$\frac{1}{2}$)2=$\frac{5}{4}$,
开方,得
x-$\frac{1}{2}$=±$\frac{\sqrt{5}}{2}$,
x1=$\frac{1}{2}$+$\frac{\sqrt{5}}{2}$,x2=$\frac{1}{2}$-$\frac{\sqrt{5}}{2}$;
(3)移项,得
2x2-5x=-1,
二次项系数化为1,得
x2-$\frac{5}{2}$x=-$\frac{1}{2}$
配方,得
(x-$\frac{5}{4}$)2=$\frac{17}{16}$,
开方,得
x-$\frac{5}{4}$=±$\frac{\sqrt{17}}{4}$,
x1=$\frac{5+\sqrt{17}}{4}$,x2=$\frac{5-\sqrt{17}}{4}$;
(4)移项,得
4x2-2x=1,
二次项系数化为1,得
x2-$\frac{1}{2}$x=$\frac{1}{4}$,
配方,得
(x-$\frac{1}{4}$)2=$\frac{5}{16}$,
开方,得
x-$\frac{1}{4}$=±$\frac{\sqrt{5}}{4}$,
x1=$\frac{1+\sqrt{5}}{4}$,x2=$\frac{1-\sqrt{5}}{4}$.
点评 本题考查了配方法解一元二次方程,配方法的一般步骤:把常数项移到等号的右边;把二次项的系数化为1;等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.


科目:初中数学 来源: 题型:解答题
 如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象.
如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
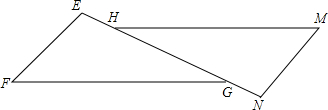 如图,△EFG≌△NMH,∠F和∠M是对应角,在△EFG中,FG是最长边,在△NMH中,MH是最长边,EF=2.1cm,EH=1.1cm,NH=3.3cm.
如图,△EFG≌△NMH,∠F和∠M是对应角,在△EFG中,FG是最长边,在△NMH中,MH是最长边,EF=2.1cm,EH=1.1cm,NH=3.3cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com