
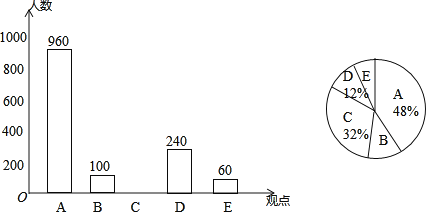
【题目】某公益机构为了解市民使用“手机阅读”的情况,对部分市民进行了随机问卷调查(问卷调查表如左图所示),并将调查结果绘制成两副统计图(均不完整)
您如何看待手机阅读问卷调查表 您好!请在表格中选择一项您最认同的观点,在其后面空格内打“√”,非常感谢您的配合. | ||
选项 | 观点 | 您的选择 |
A | 更新及时 | □ |
B | 阅读成本低 | □ |
C | 不利于人际交往 | □ |
D | 内容丰富 | □ |
E | 其他 | □ |
(1)本次接受调查的总人数是______人.
(2)请将条形统计图补充完整.
(3)在扇形统计图中,表示观点B的扇形的圆心角度数为______度.
(4)根据上述调查结果,请估计在2万名市民中,认为手机阅读“内容丰富“的大约有______人.
【答案】(1)2000;(2)详见解析;(3)18°;(4)2400.
【解析】
(1)从条形图中可知A类人数为960人,从扇形图中可知A类比例为48%,结合起来即可求出总人数;
(2)将总人数减去A、B、D、E的人数,可得C类的人数,即可根据人数画出条形;
(3)求出观点B的人数占总人数的比例,再乘以360°,即可算出表示观点B的扇形的圆心角度数;
(4)根据观点D的人数比例即可估算在2万名市民中,认为手机阅读“内容丰富“的人数.
解:(1)960÷48%=2000
即调查的总人数为2000人.
故答案为2000.
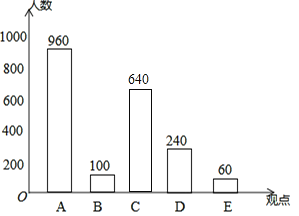
(2)持观点C的人为:2000-960-100-240-60=640,补全图形如下图所示.
(3)![]() ×360°=18°
×360°=18°
即表示观点B的扇形的圆心角度数为18°.
故答案为18.
(4)由扇形图可知认为手机阅读“内容丰富“的比例为12%,于是
在2万名市民中,认为手机阅读“内容丰富“的人数约为:20000×12%=2400
故答案为2400.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
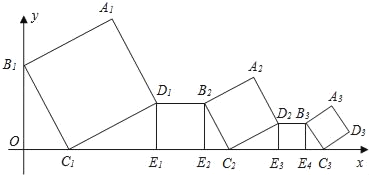
【题目】在平面直角坐标系中,正方形A1B1C1D1,D1E1E2B2,A2D2C2D2,D2E3E4B3,A3B3C3D3,…,按如图所示的方式放置,其中点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3,…,在x轴上已知正方形A1,B1,C1,D1,的边长为1,∠OB1C1=30°,B1C1∥B2C2∥B3C3,…,则正方形AnBnnDn的边长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
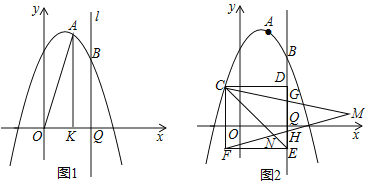
【题目】已知:如图,二次函数y=ax2+bx+![]() 的图象经过点A(2,6)和B(4,4),直线l经过点B并与x轴垂直,垂足为Q.
的图象经过点A(2,6)和B(4,4),直线l经过点B并与x轴垂直,垂足为Q.
(1)求二次函数的表达式;
(2)如图1,作AK⊥x轴,垂足为K,连接AO,点R是直线1上的点,如果△AOK与以O,Q,R为顶点的三角形相似,请直接写出点R的纵坐标;
(3)如图2,正方形CDEF的顶点C是第二象限抛物线上的点,点D,E在直线1上,以CF为底向右做等腰△CFM,直线l与CM,FM的交点分别是G,H,并且CG=GM,FH=HM,连接CE,与FM的交点为N,且点N的纵坐标是﹣1.
求:①tan∠DCG的值;
②点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
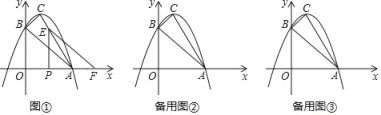
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴的一个交点为A(3,0).与y轴的交点为B(0,3),其顶点为C.
(1)求抛物线的解析式;
(2)将△AOB沿x轴向右平移m个长度单位(0<m<3)后得到另一个△FPE,点A、O、B的像分别为点F、P、E.
①如图①,当点E在直线AC上时,求m的值.
②设所得的三角形△FPE与△ABC重叠部分的面积为S,求S关于m的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班6个合作小组的人数分别是4,6,4,5,7,8,现第4小组调出1人去第2小组,则新各组人数分别为:4,7,4,4,7,8,下列关于调配后的数据说法正确的是( )
A. 调配后平均数变小了B. 调配后众数变小了
C. 调配后中位数变大了D. 调配后方差变大了
查看答案和解析>>
科目:初中数学 来源: 题型:
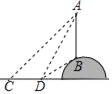
【题目】如图,为了测量小山顶的铁塔AB高度,王华和杨丽在平地上的C点处测得A点的仰角为45°,向前走了18m后到达D点,测得A点的仰角为60°,B点的仰角为30°
(1)求证:AB=BD;
(2)求证铁塔AB的高度.(结果精确到0.1米,其中![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
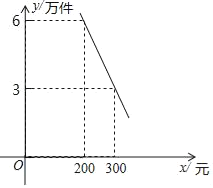
【题目】某公司每月生产产品A4万件和同类新型产品B若干万件.产品A每件销售利润为200元,且在产品B销售量每月不超过3万件时,每月4万件产品A能全部销售,产品B的每月销售量y(万件)与每件销售利润x(元)之间的函数关系图象如图所示.
(1)求y与x的函数关系式;
(2)在保证A产品全部销售的情况下,产品B每件利润定为多少元时公司销售产品A和产品B每月可获得总利润w1(万元)最大?
(3)在不要求产品A全部销售的情况下,已知受产品B销售价的影响产品A每月销售量:(万件)与x(元)之间满足关系z=0.024x﹣3.2,那么产品B每件利润定为多少元时,公司每月可获得最大的利润?并求最大总利润w2(万元).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初二年级数学考试,(满分为100分,该班学生成绩均不低于50分)作了统计分析,绘制成如图频数分布直方图和频数、频率分布表,请你根据图表提供的信息,解答下列问题:
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
频数 | 2 | a | 20 | 16 | 4 | 50 |
频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |

(1)频数、频率分布表中a= ,b= ;(答案直接填在题中横线上)
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com