
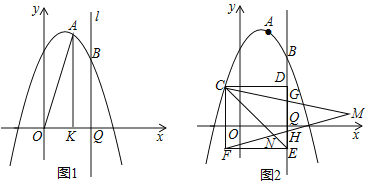
【题目】已知:如图,二次函数y=ax2+bx+![]() 的图象经过点A(2,6)和B(4,4),直线l经过点B并与x轴垂直,垂足为Q.
的图象经过点A(2,6)和B(4,4),直线l经过点B并与x轴垂直,垂足为Q.
(1)求二次函数的表达式;
(2)如图1,作AK⊥x轴,垂足为K,连接AO,点R是直线1上的点,如果△AOK与以O,Q,R为顶点的三角形相似,请直接写出点R的纵坐标;
(3)如图2,正方形CDEF的顶点C是第二象限抛物线上的点,点D,E在直线1上,以CF为底向右做等腰△CFM,直线l与CM,FM的交点分别是G,H,并且CG=GM,FH=HM,连接CE,与FM的交点为N,且点N的纵坐标是﹣1.
求:①tan∠DCG的值;
②点C的坐标.
【答案】(1)y=﹣![]() ;(2)点R的纵坐标为12,﹣12,
;(2)点R的纵坐标为12,﹣12,![]() 或﹣
或﹣![]() ;(3)①tan∠DCG的值是
;(3)①tan∠DCG的值是![]() ,②点C坐标为(﹣1,3).
,②点C坐标为(﹣1,3).
【解析】
(1)将点A(2,6)和B(4,4)代入抛物线解析式,得方程组,解得a和b,再代回原解析式即可;
(2)设点R的纵坐标为n,则QN=|n|,分两种情况,根据相似关系列比例式即可解得;
(3)①由三角形的中位线,及证Rt△CDG≌Rt△FEH (HL)可解;
②先根据点C在抛物线上,设其横坐标为m,然后用其分别表示出相关点的坐标,并表示出直线CE,再根据△CFN∽△EHN,及相似三角形对应边上的高之比也等于相似比,从而建立关于m的方程,解之,然后代回点C即可.
(1)将点A(2,6)和B(4,4)代入y=ax2+bx+![]() 得:
得:
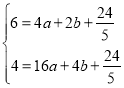 ,解得
,解得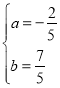
∴二次函数的表达式为y=![]() .
.
(2)∵A(2,6),AK⊥x轴,
∴K(2,0),
△AOK中,OK=2,AK=6,OA=![]() ,
,
△OQR中,OQ=4,
设点R的纵坐标为n,则QN=|n|,
如果△AOK与以O,Q,R为顶点的三角形相似,有两种情况:
①![]() ,则n=±12;
,则n=±12;
②![]() ,则
,则![]() ,从而n=±
,从而n=±![]() .
.
答:点R的纵坐标为,12,﹣12,![]() 或﹣
或﹣![]() .
.
(3)①∵CG=GM,FH=HM,
∴GH∥CF,GH=![]() CF,
CF,
∵等腰△CFM,
∴CG=FH,
∵CDEF为正方形,
∴CD=EF,∠CDG=∠FEH=90°,
∴Rt△CDG≌Rt△FEH (HL),
∴DG=EH,
∵GH=![]() CF,
CF,
∴DG=EH=![]() CF=
CF=![]() CD,
CD,
∴tan∠DCG=![]() =
=![]() ,
,
答:tan∠DCG的值是![]() .
.
②∵C是第二象限抛物线y=![]() 上的点,
上的点,
∴设点C坐标为(m,![]() ),则DC=4﹣m,
),则DC=4﹣m,
∴F(m,![]() ﹣4+m),即F(m,
﹣4+m),即F(m,![]() ),
),
∴E(4,![]() ),
),
∵CDEF为正方形,
∴∠DEC=45°,
故可设CE解析式为:y=﹣x+b,将点E坐标代入得b=![]() .
.
∴CE解析式为:y=﹣x﹣![]() ,
,
∵点N的纵坐标是﹣1,
∴﹣1=﹣x﹣![]() ,x=﹣
,x=﹣![]() ,
,
∴点N坐标为(﹣![]() ,﹣1),
,﹣1),
∵CDEF为正方形,
∴CF∥EH,
∴△CFN∽△EHN,
∵tan∠DCG=![]() =
=![]() ,DG=EH,CD=CF,
,DG=EH,CD=CF,
∴![]() ,则EH边上的高与CF边上的高的比值也为
,则EH边上的高与CF边上的高的比值也为![]() ,
,
∴![]() ,
,
化简得:﹣2m2+11m+13=0,解得m=![]() (舍)或m=﹣1,
(舍)或m=﹣1,
∴点C坐标为(﹣1,3).
答:点C坐标为(﹣1,3).


科目:初中数学 来源: 题型:
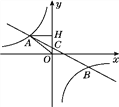
【题目】【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
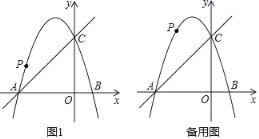
【题目】如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,A点的坐标为(﹣3,0),B点在原点的左侧,与y轴交于点C(0,3),点P是直线BC上方的抛物线上一动点
(1)求这个二次函数的表达式;
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C(如图1所示),那么是否存在点P,使四边形POP′C为菱形?若存在,请此时点P的坐标:若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABCP的面积最大,并求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
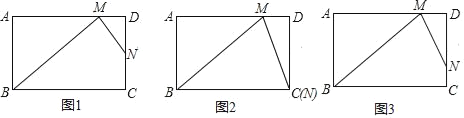
【题目】已知矩形ABCD,作∠ABC的平分线交AD边于点M,作∠BMD的平分线交CD边于点N.
(1)若N为CD的中点,如图1,求证:BM=AD+DM;
(2)若N与C点重合,如图2,求tan∠MCD的值;
(3)若![]() ,AB=6,如图3,求BC的长.
,AB=6,如图3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
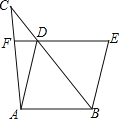
【题目】如图,在△ABC中,点D在BC边上,BC=3CD,分别过点B,D作AD,AB的平行线,并交于点E,且ED交AC于点F,AD=3DF.
(1)求证:△CFD∽△CAB;
(2)求证:四边形ABED为菱形;
(3)若DF=![]() ,BC=9,求四边形ABED的面积.
,BC=9,求四边形ABED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
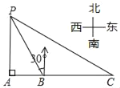
【题目】如图所示,某海盗船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处使,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,求出此时海监船与岛屿P之间的距离(即PC的长,结果精确到0.1)(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
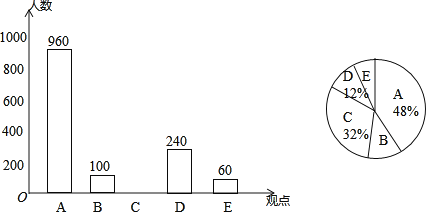
【题目】某公益机构为了解市民使用“手机阅读”的情况,对部分市民进行了随机问卷调查(问卷调查表如左图所示),并将调查结果绘制成两副统计图(均不完整)
您如何看待手机阅读问卷调查表 您好!请在表格中选择一项您最认同的观点,在其后面空格内打“√”,非常感谢您的配合. | ||
选项 | 观点 | 您的选择 |
A | 更新及时 | □ |
B | 阅读成本低 | □ |
C | 不利于人际交往 | □ |
D | 内容丰富 | □ |
E | 其他 | □ |
(1)本次接受调查的总人数是______人.
(2)请将条形统计图补充完整.
(3)在扇形统计图中,表示观点B的扇形的圆心角度数为______度.
(4)根据上述调查结果,请估计在2万名市民中,认为手机阅读“内容丰富“的大约有______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年足球亚洲杯正在阿联酋进行,这项起源于我国“蹴鞠”的运动项目近年来在我国中小学校园得到大力推广,某次校园足球比赛规定:胜一场得3分,平一场得1分,负一场得0分,某足球队共进行了8场比赛,得了12分,该队获胜的场数有几种可能( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com