
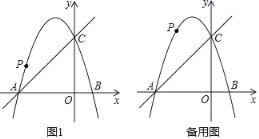
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§yЃНЉx2+bx+cЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌAЕуЕФзјБъЮЊЃЈЉ3ЃЌ0ЃЉЃЌBЕудкдЕуЕФзѓВрЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ3ЃЉЃЌЕуPЪЧжБЯпBCЩЯЗНЕФХзЮяЯпЩЯвЛЖЏЕу
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉСЌНгPOЁЂPCЃЌВЂАбЁїPOCбиCOЗелЃЌЕУЕНЫФБпаЮPOPЁфCЃЈШчЭМ1ЫљЪОЃЉЃЌФЧУДЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮPOPЁфCЮЊСтаЮЃПШєДцдкЃЌЧыДЫЪБЕуPЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЫФБпаЮABCPЕФУцЛ§зюДѓЃЌВЂЧѓГіЦфзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2Љ2x+3ЃЛЃЈ2ЃЉДцдкЃЎPЕуЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉPЕуЕФзјБъЮЊЃЈЉ
ЃЉЃЛЃЈ3ЃЉPЕуЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЫФБпаЮABPCЕФУцЛ§ЕФзюДѓжЕЮЊ
ЃЉЃЌЫФБпаЮABPCЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈжБНгНЋBЁЂCСНЕужБНгДњШыyЃНx2+bx+cЧѓНтbЃЌcЕФжЕМДПЩЕУХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉРћгУСтаЮЖдНЧЯпЕФаджЪМАелЕўЕФаджЪПЩвдХаЖЯPЕуЕФзнзјБъЮЊЉ![]() ЃЌСюyЃНЉ
ЃЌСюyЃНЉ![]() МДПЩЕУx2Љ2xЉ3ЃНЉ
МДПЩЕУx2Љ2xЉ3ЃНЉ![]() ЃЌНтИУЗНГЬМДПЩШЗЖЈPЕузјБъЃЛ
ЃЌНтИУЗНГЬМДПЩШЗЖЈPЕузјБъЃЛ
ЃЈ3ЃЉгЩгкЁїABCЕФУцЛ§ЮЊЖЈжЕЃЌЕБЫФБпаЮABCPЕФУцЛ§зюДѓЪБЃЌЁїBPCЕФУцЛ§зюДѓЃЛЙ§PзїyжсЕФЦНааЯпЃЌНЛжБЯпBCгкQЃЌНЛxжсгкFЃЌвзЧѓЕУжБЯпACЕФНтЮіЪНЃЌПЩЩшГіPЕуЕФКсзјБъЃЌШЛКѓИљОнХзЮяЯпКЭжБЯпBCЕФНтЮіЪНЧѓГіQЁЂPЕФзнзјБъЃЌМДПЩЕУЕНPQЕФГЄЃЌвдPQЮЊЕзЃЌBЕуКсзјБъЕФОјЖджЕЮЊИпМДПЩЧѓЕУЁїBPCЕФУцЛ§ЃЌгЩДЫПЩЕУЕНЙигкЫФБпаЮABCPЕФУцЛ§гыPЕуКсзјБъЕФКЏЪ§ЙиЯЕЪНЃЌИљОнКЏЪ§ЕФаджЪМДПЩЧѓГіЫФБпаЮABCPЕФзюДѓУцЛ§МАЖдгІЕФPЕузјБъЃЎ
ЃЈ1ЃЉЁпCЕузјБъЮЊЃЈ0ЃЌ3ЃЉЃЌ
ЁрyЃНЉx2+bx+3ЃЌ
АбAЃЈЉ3ЃЌ0ЃЉДњШыЩЯЪНЕУЃЌ0ЃН9Љ3b+3ЃЌ
НтЕУЃЌbЃНЉ2ЃЌ
ЁрИУЖўДЮКЏЪ§НтЮіЪНЮЊЃКyЃНЉx2Љ2x+3ЃЛ
ЃЈ2ЃЉДцдкЃЎШчЭМ1ЃЌ
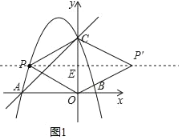
ЩшPЕуЕФзјБъЮЊЃЈxЃЌЉx2Љ2x+3ЃЉЃЌPPЁфНЛCOгкEЃЌ
ЕБЫФБпаЮPOP'CЮЊСтаЮЪБЃЌдђгаPCЃНPOЃЌСЌНгPPЁфЃЌдђPEЁЭCOгкEЃЌ
ЁрOEЃНCEЃН![]() ЃЌ
ЃЌ
СюЉx2Љ2x+3ЃН![]() ЃЌ
ЃЌ
НтЕУЃЌx1ЃНЉ![]() ЃЌx2ЃН
ЃЌx2ЃН![]() ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЎ
ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЎ
ЁрPЕуЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§ЕуPзїyжсЕФЦНааЯпгыBCНЛгкЕуQЃЌгыOAНЛгкЕуFЃЌ
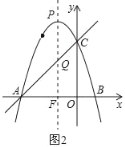
ЩшPЃЈxЃЌЉx2Љ2x+3ЃЉЃЌЩшжБЯпACЕФНтЮіЪНЮЊЃКyЃНkx+tЃЌ
дђ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊyЃНx+3ЃЌ
дђQЕуЕФзјБъЮЊЃЈxЃЌx+3ЃЉЃЌ
ЕБ0ЃНЉx2Љ2x+3ЃЌ
НтЕУЃКx1ЃН1ЃЌx2ЃНЉ3ЃЌ
ЁрAOЃН3ЃЌOBЃН1ЃЌдђABЃН4ЃЌ
SЫФБпаЮABCPЃНSЁїABC+SЁїAPQ+SЁїCPQ
ЃН![]() ABOC+
ABOC+![]() QPOF+
QPOF+![]() QPAF
QPAF
ЃН![]() ЁС4ЁС3+
ЁС4ЁС3+![]() [ЃЈЉx2Љ2x+3ЃЉЉЃЈx+3ЃЉ]ЁС3
[ЃЈЉx2Љ2x+3ЃЉЉЃЈx+3ЃЉ]ЁС3
ЃНЉ![]() ЃЈx+
ЃЈx+![]() ЃЉ2+
ЃЉ2+![]() ЃЎ
ЃЎ
ЕБxЃНЉ![]() ЪБЃЌЫФБпаЮABCPЕФУцЛ§зюДѓЃЌ
ЪБЃЌЫФБпаЮABCPЕФУцЛ§зюДѓЃЌ
ДЫЪБPЕуЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЫФБпаЮABPCЕФУцЛ§ЕФзюДѓжЕЮЊ
ЃЉЃЌЫФБпаЮABPCЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
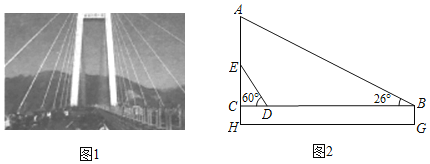
ЁОЬтФПЁПББХЬНДѓЧХзјТфгкдЦФЯвЫЭўгыЙѓжнЫЎГЧНЛНчДІЃЌКсПчдЦЙѓСНЪЁЃЌЮЊФПЧАЪРНчЕквЛИпЧХЭМ1ЪЧДѓЧХЕФЪЕЮяЭМЃЌЭМ2ЪЧДгЭМ1жав§ЩъГіЕФЦНУцЭМЃЌВтЕУЧХЛЄРИBG=1.8УзЃЌРЫїABгыЛЄРИЕФМаНЧЪЧ26ЁуЃЌРЫїEDгыЛЄРИЕФМаНЧЪЧ60ЁуЃЌСНРЫїЕзЖЫОрРыBDЮЊ300mЃЌШєСНРЫїЖЅЖЫЕФОрРыAEЮЊ90mЃЌЧыЧѓГіСЂжљAHЕФГЄЃЎЃЈtan26ЁуЁж0.5ЃЌsin26ЁуЁж0.4ЃЌ![]() 1.7ЃЉ
1.7ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮКЏЪ§y=kxЉ1ЕФЭМЯѓОЙ§ЕуPЃЌЧвyЕФжЕЫцxжЕЕФдіДѓЖјдіДѓЃЌдђЕуPЕФзјБъПЩвдЮЊЃЈЁЁЁЁЃЉ
A. ЃЈЉ5ЃЌ3ЃЉ B. ЃЈ1ЃЌЉ3ЃЉ C. ЃЈ2ЃЌ2ЃЉ D. ЃЈ5ЃЌЉ1ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
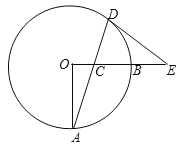
ЁОЬтФПЁПШчЭМЃЌOAЁЂOBЪЧЁбOЕФСНЬѕАыОЖЃЌOAЁЭOBЃЌCЪЧАыОЖOBЩЯвЛЖЏЕуЃЌСЌНгACВЂбгГЄНЛЁбOгкDЃЌЙ§ЕуDзїдВЕФЧаЯпНЛOBЕФбгГЄЯпгкEЃЌвбжЊOAЃН6ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯECDЃНЁЯEDCЃЛ
ЃЈ2ЃЉШєBCЃН2OCЃЌЧѓDEГЄЃЛ
ЃЈ3ЃЉЕБЁЯAДг15ЁудіДѓЕН30ЁуЕФЙ§ГЬжаЃЌЧѓЯвADдкдВФкЩЈЙ§ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓЕФЖдГЦжсЪЧжБЯпxЃН1ЃЌЦфЭМЯѓЕФвЛВПЗжШчЭМЫљЪОЃЎЯТСаЫЕЗЈДэЮѓЕФЪЧ
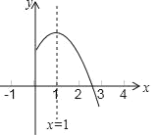
A. abcЃМ0B. aЉb+cЃМ0C. 3a+cЃМ0D. ЕБЉ1ЃМxЃМ3ЪБЃЌyЃО0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬтТњЗж8ЗжЃЉ
ЮЊСЫМгЧПбЇЩњПЮЭтдФЖСЃЌПЊРЋЪгвАЃЌФГаЃПЊеЙСЫЁАЪщЯуаЃдАЃЌДгЮвзіЦ№ЁБЕФжїЬтЛюЖЏЃЎбЇаЃЫцЛњГщШЁСЫВПЗжбЇЩњЃЌЖдЫћУЧвЛжмЕФПЮЭтдФЖСЪБМфНјааЕїВщЃЌЛцжЦГіЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМЕФвЛВПЗжШчЯТЃК
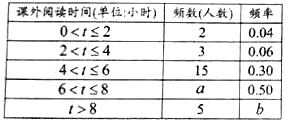
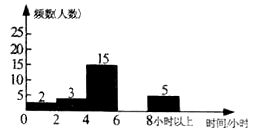
ЧыИљОнЭМБэаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЦЕЪ§ЗжВМБэжаЕФ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉбЇаЃНЋУПжмПЮЭтдФЖСЪБМфдк![]() аЁЪБвдЩЯЕФбЇЩњЦРЮЊЁАдФЖСжЎаЧЁБЃЌЧыФуЙРМЦИУаЃ
аЁЪБвдЩЯЕФбЇЩњЦРЮЊЁАдФЖСжЎаЧЁБЃЌЧыФуЙРМЦИУаЃ![]() УћбЇЩњжаЦРЮЊЁАдФЖСжЎаЧЁБЕФгаЖрЩйШЫЃП
УћбЇЩњжаЦРЮЊЁАдФЖСжЎаЧЁБЕФгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌе§ЗНаЮA1B1C1D1ЃЌD1E1E2B2ЃЌA2D2C2D2ЃЌD2E3E4B3ЃЌA3B3C3D3ЃЌЁЃЌАДШчЭМЫљЪОЕФЗНЪНЗХжУЃЌЦфжаЕуB1дкyжсЩЯЃЌЕуC1ЃЌE1ЃЌE2ЃЌC2ЃЌE3ЃЌE4ЃЌC3ЃЌЁЃЌдкxжсЩЯвбжЊе§ЗНаЮA1ЃЌB1ЃЌC1ЃЌD1ЃЌЕФБпГЄЮЊ1ЃЌЁЯOB1C1ЃН30ЁуЃЌB1C1ЁЮB2C2ЁЮB3C3ЃЌЁЃЌдђе§ЗНаЮAnBnnDnЕФБпГЄЪЧЃЈЁЁЁЁЃЉ
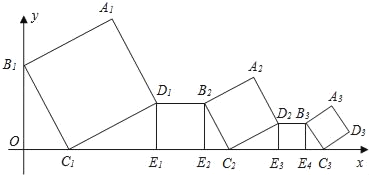
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
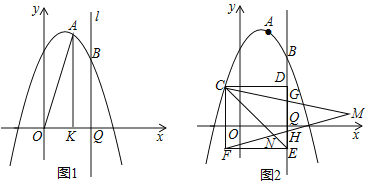
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЖўДЮКЏЪ§yЃНax2+bx+![]() ЕФЭМЯѓОЙ§ЕуAЃЈ2ЃЌ6ЃЉКЭBЃЈ4ЃЌ4ЃЉЃЌжБЯпlОЙ§ЕуBВЂгыxжсДЙжБЃЌДЙзуЮЊQЃЎ
ЕФЭМЯѓОЙ§ЕуAЃЈ2ЃЌ6ЃЉКЭBЃЈ4ЃЌ4ЃЉЃЌжБЯпlОЙ§ЕуBВЂгыxжсДЙжБЃЌДЙзуЮЊQЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌзїAKЁЭxжсЃЌДЙзуЮЊKЃЌСЌНгAOЃЌЕуRЪЧжБЯп1ЩЯЕФЕуЃЌШчЙћЁїAOKгывдOЃЌQЃЌRЮЊЖЅЕуЕФШ§НЧаЮЯрЫЦЃЌЧыжБНгаДГіЕуRЕФзнзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌе§ЗНаЮCDEFЕФЖЅЕуCЪЧЕкЖўЯѓЯоХзЮяЯпЩЯЕФЕуЃЌЕуDЃЌEдкжБЯп1ЩЯЃЌвдCFЮЊЕзЯђгвзіЕШбќЁїCFMЃЌжБЯпlгыCMЃЌFMЕФНЛЕуЗжБ№ЪЧGЃЌHЃЌВЂЧвCGЃНGMЃЌFHЃНHMЃЌСЌНгCEЃЌгыFMЕФНЛЕуЮЊNЃЌЧвЕуNЕФзнзјБъЪЧЉ1ЃЎ
ЧѓЃКЂйtanЁЯDCGЕФжЕЃЛ
ЂкЕуCЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
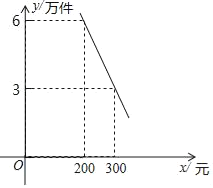
ЁОЬтФПЁПФГЙЋЫОУПдТЩњВњВњЦЗA4ЭђМўКЭЭЌРраТаЭВњЦЗBШєИЩЭђМўЃЎВњЦЗAУПМўЯњЪлРћШѓЮЊ200дЊЃЌЧвдкВњЦЗBЯњЪлСПУПдТВЛГЌЙ§3ЭђМўЪБЃЌУПдТ4ЭђМўВњЦЗAФмШЋВПЯњЪлЃЌВњЦЗBЕФУПдТЯњЪлСПyЃЈЭђМўЃЉгыУПМўЯњЪлРћШѓxЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЭМЯѓШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉдкБЃжЄAВњЦЗШЋВПЯњЪлЕФЧщПіЯТЃЌВњЦЗBУПМўРћШѓЖЈЮЊЖрЩйдЊЪБЙЋЫОЯњЪлВњЦЗAКЭВњЦЗBУПдТПЩЛёЕУзмРћШѓw1ЃЈЭђдЊЃЉзюДѓЃП
ЃЈ3ЃЉдкВЛвЊЧѓВњЦЗAШЋВПЯњЪлЕФЧщПіЯТЃЌвбжЊЪмВњЦЗBЯњЪлМлЕФгАЯьВњЦЗAУПдТЯњЪлСПЃКЃЈЭђМўЃЉгыxЃЈдЊЃЉжЎМфТњзуЙиЯЕzЃН0.024xЉ3.2ЃЌФЧУДВњЦЗBУПМўРћШѓЖЈЮЊЖрЩйдЊЪБЃЌЙЋЫОУПдТПЩЛёЕУзюДѓЕФРћШѓЃПВЂЧѓзюДѓзмРћШѓw2ЃЈЭђдЊЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com