
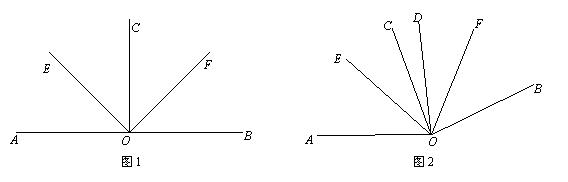
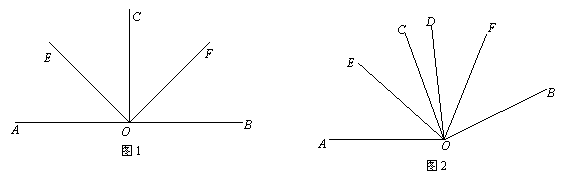
(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC. 求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= .(用含α与β的代数式表示)
 |
(1) ∵CO⊥AB,
∴∠AOC=∠BOC=90°……………………1分
∵OE平分∠AOC,∴∠EOC= ∠AOC=
∠AOC= ×90°=45°;
×90°=45°;
∵OF平分∠BOC,∴∠COF= ∠BOC=
∠BOC= ×90°=45°;……………………2分
×90°=45°;……………………2分
∠EOF=∠EOC+∠COF=45°+45°=90°;……………………3分
(2)∵OE平分∠AOD,∴∠EOD= ∠AOD=
∠AOD= ×(80+β)=40+
×(80+β)=40+ β;………………4分
β;………………4分
∵OF平分∠BOC,∴∠COF= ∠BOC=
∠BOC= ×(80+β)=40+
×(80+β)=40+ β;……………………5分
β;……………………5分
∠COE=∠EOD-∠COD=40+ β-β=40-
β-β=40- β;
β;
∠EOF=∠COE+∠COF=40- β+40+
β+40+ β=80°. ……………………6分
β=80°. ……………………6分
 (3)
(3) a±
a± β (一个1分) ……………………8分
β (一个1分) ……………………8分


科目:初中数学 来源: 题型:
学习直线、射线、线段和线段中点等内容之后,王老师请同学们交流这样一个问题:“射线OA上有B,C两点,若OB=8,BC=2,点D是线段OB的中点,请你求出线段DC的长.”张华同学通过计算得到DC的长是6,你认为张华的答案是否正确 ,你的理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
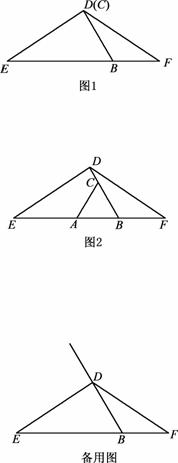
在△DEF中,DE=DF,点B在EF边上,且∠EBD=60°,C是射线BD上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为 ;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD的延长线上时,用等式表示线段AE ,BF ,CD之间的数量关系(直接写出结果,不需要证明).
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
运动会前夕,爸爸陪小明在400m的环形跑道上训练,他们在同一地点沿着同一方向同
时出发.
 | |||
 | |||


(1)请根据他们的对话内容,求出小明和爸爸的速度;
(2)爸爸追上小明后,在第二次相遇前,再经过 分钟,小明和爸爸在跑道上相距50m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com