
如图,在平面直角坐标系中,顶点为(4,﹣1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).
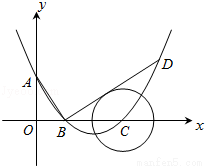
(1)求此抛物线的解析式
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;
(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.
(1)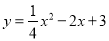 ;(2)相交.证明见解析;(3)当m=3时,△PAC的面积最大为
;(2)相交.证明见解析;(3)当m=3时,△PAC的面积最大为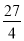 ;此时,P点的坐标为(3,-
;此时,P点的坐标为(3,-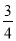 ).
).
【解析】
试题分析:(1)已知抛物线的顶点坐标,可用顶点式设抛物线的解析式,然后将A点坐标代入其中,即可求出此二次函数的解析式;
(2)根据抛物线的解析式,易求得对称轴l的解析式及B、C的坐标,分别求出直线AB、BD、CE的解析式,再求出CE的长,与到抛物线的对称轴的距离相比较即可;
(3)过P作y轴的平行线,交AC于Q;易求得直线AC的解析式,可设出P点的坐标,进而可表示出P、Q的纵坐标,也就得出了PQ的长;然后根据三角形面积的计算方法,可得出关于△PAC的面积与P点横坐标的函数关系式,根据所得函数的性质即可求出△PAC的最大面积及对应的P点坐标.
试题解析:(1)设抛物线为y=a(x﹣4)2﹣1,
∵抛物线经过点A(0,3),
∴3=a(0﹣4)2﹣1,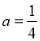 ;
;
∴抛物线为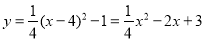
(2)相交.
证明:连接CE,则CE⊥BD,
当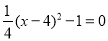 时,x1=2,x2=6.
时,x1=2,x2=6.
A(0,3),B(2,0),C(6,0),
对称轴x=4,
∴OB=2,AB=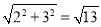 ,BC=4,
,BC=4,
∵AB⊥BD,
∴∠OAB+∠OBA=90°,∠OBA+∠EBC=90°,
∴△AOB∽△BEC,
∴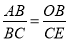 ,
,
即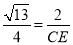 ,
,
解得CE=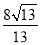 ,
,
∵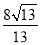 >2,
>2,
∴抛物线的对称轴l与⊙C相交.(7分)
(3)如图,过点P作平行于y轴的直线交AC于点Q;
可求出AC的解析式为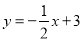
设P点的坐标为(m,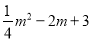 ),
),
则Q点的坐标为(m,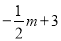 );
);
∴PQ=﹣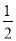 m+3﹣(
m+3﹣(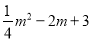 )=﹣
)=﹣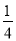 m2+
m2+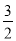 m.
m.
∵S△PAC=S△PAQ+S△PCQ=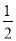 ×(﹣
×(﹣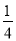 m2+
m2+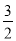 m)×6
m)×6
=-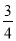 (m﹣3)2+
(m﹣3)2+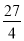 ;
;
∴当m=3时,△PAC的面积最大为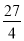 ;
;
此时,P点的坐标为(3,-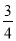 ).
).
考点:二次函数综合题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年四川省九年级一诊数学试卷(解析版) 题型:解答题
学习了统计知识后,班主任王老师叫班长就本班同学的上学方式进行了一次调查统计,图1和图2是他通过收集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题: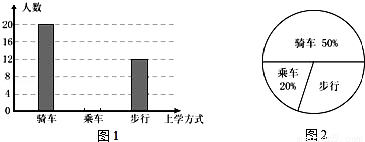
(1)在扇形统计图中,计算出“步行”部分所对应的圆心角的度数;
(2)求该班共有多少名学生;
(3)在图1中,将表示“乘车”的部分补充完整.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级一诊数学试卷(解析版) 题型:选择题
二次函数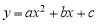 的图象如图所示,则下列关系式不正确的是( )
的图象如图所示,则下列关系式不正确的是( )
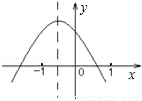
A.a<0 B.abc>0 C.a+b+c>0 D.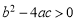
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级一诊数学试卷(解析版) 题型:选择题
为了估计湖中有多少条鱼,先从湖中捕捉50条鱼做记号,然后放回湖里,经过一段时间,等带记号的鱼完全混于鱼群中之后,再捕捞第二次,鱼共200条,有10条做了记号,则估计湖里有多少条鱼( )
A.400条 B.500条 C.800条 D.1000条
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省日照市莒县北五校九年级上学期12月联考数学试卷(解析版) 题型:解答题
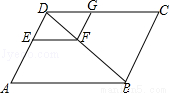
(10分)如图,在?ABCD中,EF∥AB,FG∥ED,DE∶EA=2∶3,EF=4,求线段CG的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省丹东市九年级上学期第二次月考数学试卷(解析版) 题型:选择题
用配方法解方程x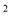 -4x-2=0,变形后为( )
-4x-2=0,变形后为( )
A、(x-2)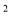 = 6 B、(x-4)
= 6 B、(x-4)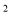 = 6 C、(x-2)
= 6 C、(x-2)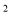 = 2 D、(x+2)
= 2 D、(x+2)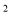 = 6
= 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com