
【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( ) 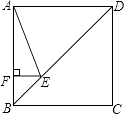
A.1
B.![]()
C.4﹣2 ![]()
D.3 ![]() ﹣4
﹣4
【答案】C
【解析】解:在正方形ABCD中,∠ABD=∠ADB=45°, ∵∠BAE=22.5°,
∴∠DAE=90°﹣∠BAE=90°﹣22.5°=67.5°,
在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,
∴∠DAE=∠AED,
∴AD=DE=4,
∵正方形的边长为4,
∴BD=4 ![]() ,
,
∴BE=BD﹣DE=4 ![]() ﹣4,
﹣4,
∵EF⊥AB,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴EF= ![]() BE=
BE= ![]() ×(4
×(4 ![]() ﹣4)=4﹣2
﹣4)=4﹣2 ![]() .
.
故选:C.
根据正方形的对角线平分一组对角可得∠ABD=∠ADB=45°,再求出∠DAE的度数,根据三角形的内角和定理求∠AED,从而得到∠DAE=∠AED,再根据等角对等边的性质得到AD=DE,然后求出正方形的对角线BD,再求出BE,最后根据等腰直角三角形的直角边等于斜边的 ![]() 倍计算即可得解.
倍计算即可得解.


科目:初中数学 来源: 题型:
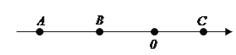
【题目】如图,数轴上有A、B、C三个点,A、B、C对应的数分别是a、b、c,且满足![]() +
+![]() +(c-10)2=0,动点P从A出发,以每秒1个单位的速度向终点C运动,设运动时间为t秒.
+(c-10)2=0,动点P从A出发,以每秒1个单位的速度向终点C运动,设运动时间为t秒.
(1)求a、b、c的值;
(2)若点P到A点的距离是点P到B点的距离的2倍,求点P对应的数;
(3)当点P运动到B点时,点Q从点A出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后第几秒时,P、Q两点之间的距离为4?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE. 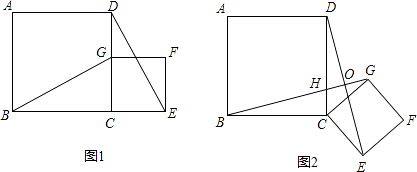
(1)猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;
(2)将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“自驾游”已成为人们出游的重要方式.“十一”国庆节,某老师驾轿车从舟山出发,上高速公路途经舟山跨海大桥和杭州湾跨海大桥到嘉兴下高速,其间用了4.5小时;返回时平均速度提高了10千米/小时,比去时少用了半小时回到舟山.
(1)求舟山与嘉兴两地间的高速公路路程;
(2)两座跨海大桥的长度及过桥费见下表:
大桥名称 | 舟山跨海大桥 | 杭州湾跨海大桥 |
大桥长度 | 48千米 | 36千米 |
过桥费 | 100元 | 80元 |
交通部门规定:轿车的高速公路通行费![]() (元)的计算方法为:
(元)的计算方法为: ![]() ,其中
,其中![]() (元/千米)为高速公路里程费,
(元/千米)为高速公路里程费, ![]() (千米)为高速公路里程(不包括跨海大桥长),
(千米)为高速公路里程(不包括跨海大桥长),![]() (元)为跨海大桥过桥费.若林老师从舟山到嘉兴所花的高速公路通行费为295.4元,求轿车的高速公路里程费
(元)为跨海大桥过桥费.若林老师从舟山到嘉兴所花的高速公路通行费为295.4元,求轿车的高速公路里程费![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红安卷烟厂生产的“龙乡”牌香烟盒里,装满大小均匀的20支香烟,打开烟盒的顶盖后,二十支香烟排列成三行,经测量,一支香烟的直径约为0.75cm,长约为8.4cm. 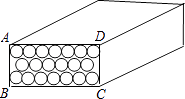
(1)试计算烟盒顶盖ABCD的面积(本小题计算结果不取近似值).
(2)制作这样一个烟盒至少需要多少面积的纸张(不计重叠粘合的部分,计算结果精确到0.1cm, ![]() 取1.73).
取1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图像与反比例函数y= ![]() 的图像交于M、N两点.
的图像交于M、N两点. 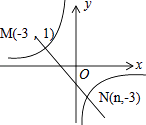
(1)求反比例函数与一次函数的解析式;
(2)根据图像写出使反比例函数的值大于一次函数的值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com