
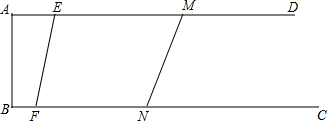
分析 (1)当EM=FN时,以E,F,N,M为顶点的四边形为平行四边形,分类讨论:当点E,F在MN的左侧时,EM=10-2t,FN=8-t,则10-2t=8-t;当点F在MN的左侧时,点E在MN的右侧时,EM=2t-10,FN=8-t,则2t-10=8-t,然后分别解方程即可得到对应的t的值;
(2)作MN的垂直平分线交AD于M,交BC于N,交MN于O点,作MQ⊥BC于Q,如图,先证明△OME≌△ONF得到EM=FN,则可判断四边形MENF为平行四边形,加上MN⊥EF,则四边形MENF为菱形,接着在Rt△MNQ中利用勾股定理计算出MN=2$\sqrt{5}$,通过Rt△OEM∽Rt△QMN,利用相似比可计算出EM=5,则NF=5,于是得到AE=AM-EM=5,BQ=BN+NF=13,然后得到点E和点F的速度比.
解答 解:(1)∵AD∥BC,
∴EM∥FN,
当EM=FN时,以E,F,N,M为顶点的四边形为平行四边形,
当点E,F在MN的左侧时,
∵AM=10cm,BN=8cm
∴EM=10-2t,FN=8-t,
∴10-2t=8-t,
解得:t=2,
当点F在MN的左侧时,点E在MN的右侧时,
∵AM=10cm,BN=8cm
∴EM=2t-10,FN=8-t,
∴2t-10=8-t,
解得:t=6,
综上所述:当t=2s或6s时,以E,F,N,M为顶点的四边形为平行四边形;
(2)作MN的垂直平分线交AD于M,交BC于N,交MN于O点,作MQ⊥BC于Q,如图,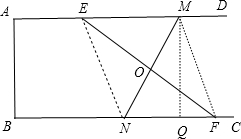
∵AD∥BC,
∴∠OEM=∠OFN,∠OME=∠ONF,
在△OME和△ONF中,
$\left\{\begin{array}{l}{∠OEM=∠OFN}\\{∠OME=∠ONF}\\{OM=ON}\end{array}\right.$,
∴△OME≌△ONF,
∴EM=FN,
而EM∥FN,
∴四边形MENF为平行四边形,
∵MN⊥EF,
∴四边形MENF为菱形,
在Rt△MNQ中,∵MQ=AB=4,NQ=BQ-BN=AM-BN=10-8=2,
∴MN=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴OM=$\sqrt{5}$,
∵∠NMQ=∠OEM,
∴Rt△OEM∽Rt△QMN,
∴$\frac{EM}{MN}$=$\frac{OM}{NQ}$,即$\frac{EM}{2\sqrt{5}}$=$\frac{\sqrt{5}}{2}$,
解得EM=5,
∴NF=5,
∴AE=AM-EM=5,BQ=BN+NF=13,
∴$\frac{{v}_{E}}{{v}_{F}}$=$\frac{5}{13}$.
故答案为:2或6;$\frac{5}{13}$.
点评 本题考查了菱形的判定:一组邻边相等的平行四边形是菱形;四条边都相等的四边形是菱形;对角线互相垂直的平行四边形是菱形(或“对角线互相垂直平分的四边形是菱形”).也考查了相似三角形的判定与性质.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
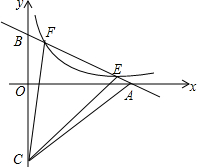 如图,直线y=-$\frac{1}{2}$x+b(b>0)与双曲线y=$\frac{1}{x}$(x>0)交于E、F两点,与x轴、y轴分别交于A、B两点,点C(0,-$\frac{3}{2}$b),连接CA,CB,CE,CF,若S△CEF=2(S△CAE+S△CBF),求b的值.
如图,直线y=-$\frac{1}{2}$x+b(b>0)与双曲线y=$\frac{1}{x}$(x>0)交于E、F两点,与x轴、y轴分别交于A、B两点,点C(0,-$\frac{3}{2}$b),连接CA,CB,CE,CF,若S△CEF=2(S△CAE+S△CBF),求b的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
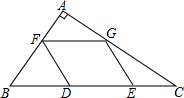 如图,在△ABC中,点D、E是BC边上的三等分点,点F在AB边上运动,点G在AC边上运动,在F、G运动过程中,若存在四边形FDEG是菱形,则△ABC必须满足的条件是( )
如图,在△ABC中,点D、E是BC边上的三等分点,点F在AB边上运动,点G在AC边上运动,在F、G运动过程中,若存在四边形FDEG是菱形,则△ABC必须满足的条件是( )| A. | AB=AC且∠A=120° | B. | △ABC为正三角形 | ||
| C. | ∠A=90° | D. | 不存在这样的三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-3,-1) | C. | (1,3) | D. | ($\frac{3}{2}$,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com