
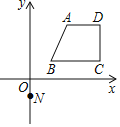
【题目】如图,过点N(0,-1)的直线y=kx+b与图中的四边形ABCD有不少于两个交点,其中A(2,3)、B(1,1)、C(4,1)、D(4,3),则k的取值范围____________
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七、八年级各选![]() 名同学参加“创全国文明城市”知识竞赛,计分
名同学参加“创全国文明城市”知识竞赛,计分![]() 分制,选手得分均为整数,成绩达到
分制,选手得分均为整数,成绩达到![]() 分或
分或![]() 分以上为合格,达到
分以上为合格,达到![]() 分或
分或![]() 分以上为优秀,这次竞赛后,七、八年级两支代表队成绩分布的条形统计图和成绩分析表如下,其中七年级代表队得
分以上为优秀,这次竞赛后,七、八年级两支代表队成绩分布的条形统计图和成绩分析表如下,其中七年级代表队得![]() 分、
分、![]() 分选手人数分别为
分选手人数分别为![]() ,
,![]() .
.
队列 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
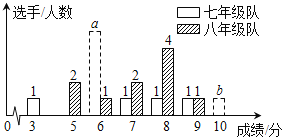
(1)根据图表中的数据,求![]() ,
,![]() 的值.
的值.
(2)直接写出表中的![]() ,
,![]() .
.
(3)你是八年级学生,请你给出两条支持八年级队成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,![]() ,且
,且![]() .
.
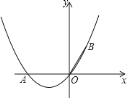
![]() 求经过
求经过![]() ,
,![]() ,
,![]() 三点的抛物线的解析式.
三点的抛物线的解析式.
![]() 在
在![]() 中抛物线的对称轴上是否存在点
中抛物线的对称轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 若点
若点![]() 为抛物线上一点,点
为抛物线上一点,点![]() 为对称轴上一点,是否存在点
为对称轴上一点,是否存在点![]() ,
,![]() 使得
使得![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形是平行四边形?若存在,求出点
构成的四边形是平行四边形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,每人射击10次,成绩分别如下:
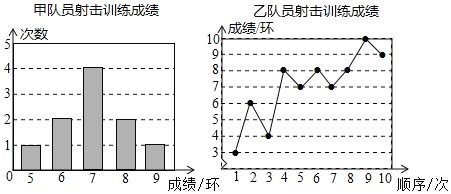
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
|
| 4.2 |
(1)![]() __________;
__________;![]() _____________;
_____________;![]() __________;
__________;
(2)填空:(填“甲”或“乙”)
①从平均数和中位数的角度来比较,成绩较好的是__________;
②从平均数和众数的角度来比较,成绩较好的是_________________;
③成绩相对较稳定的是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线
经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线![]() :
:![]() (a≠0),
(a≠0),
(1)试求抛物线![]() 的函数解析式;
的函数解析式;
(2)求证: 抛物线 ![]() 与x轴一定有两个不同的交点;
与x轴一定有两个不同的交点;
(3)若a=1
①抛物线![]() 、
、![]() 顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线
顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线![]() 、
、![]() 上的点的纵坐标同时随横坐标增大而增大;
上的点的纵坐标同时随横坐标增大而增大;
②已知直线MN分别与x轴、![]() 、
、![]() 分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。
分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
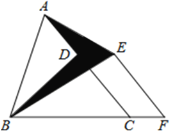
A.3B.4C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:
因式分解----“分组分解法”:分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式,比如,四项的多项式一般按照“两两”分组或“三一”分组进行分组分解.分析多项式的特点,恰当的分组是分组分解法的关键.
例1:“两两”分组:
![]()
![]()
![]()
![]()
我们把![]() 和
和![]() 两项分为一组,
两项分为一组,![]() 和
和![]() 两项分为一组,分别提公因式,立即解除了困难.同样.这道题也可以这样做:
两项分为一组,分别提公因式,立即解除了困难.同样.这道题也可以这样做:
![]()
![]()
![]()
![]()
例2:“三一”分组:
![]()
![]()
![]()
我们把![]() ,
,![]() ,
,![]() 三项分为一组,运用完全平方公式得到
三项分为一组,运用完全平方公式得到![]() ,再与-1用平方差公式分解,问题迎刃而解.
,再与-1用平方差公式分解,问题迎刃而解.
归纳总结:用分组分解法分解因式的方法是先恰当分组,然后用提公因式法或运用公式法继续分解.
请同学们在阅读材料的启发下,解答下列问题:
(1)分解因式:
①![]() ;
;
②![]()
(2)若多项式![]() 利用分组分解法可分解为
利用分组分解法可分解为![]() ,请写出
,请写出![]() ,
,![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com