
【题目】如图,在直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,![]() ,且
,且![]() .
.
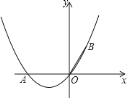
![]() 求经过
求经过![]() ,
,![]() ,
,![]() 三点的抛物线的解析式.
三点的抛物线的解析式.
![]() 在
在![]() 中抛物线的对称轴上是否存在点
中抛物线的对称轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 若点
若点![]() 为抛物线上一点,点
为抛物线上一点,点![]() 为对称轴上一点,是否存在点
为对称轴上一点,是否存在点![]() ,
,![]() 使得
使得![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形是平行四边形?若存在,求出点
构成的四边形是平行四边形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)抛物线解析式为![]() ;(2)存在,点C的坐标为
;(2)存在,点C的坐标为![]() .(3)存在,点M的坐标为:
.(3)存在,点M的坐标为:![]() 、
、![]() .
.
【解析】
试题分析: (1)先确定出点B坐标,再用待定系数法即可;
(2)先判断出使△BOC的周长最小的点C的位置,再求解即可;
(3)分OA为对角线和为边两种情况进行讨论计算.
试题解析:
(1)过点B作BD⊥x轴于点D,由已知可得:OB=OA=2,∠BOD=60°,
在Rt△OBD中,∠ODB=90°,∠OBD=30°
∴OD=1,DB=![]()
∴点B的坐标是(1,![]() ).
).
设所求抛物线的解析式为![]() ,
,
由已知可得: ,
,
解得:![]()
∴所求抛物线解析式为![]() .
.
(2)存在,
∵![]()
又∵OB=2
∴要使△BOC的周长最小,必须BC+CO最小,
∵点O和点A关于对称轴对称
∴连接AB与对称轴的交点即为点C
且有OC=OA
此时![]() ;
;
点C为直线AB与抛物线对称轴的交点
设直线AB的解析式为![]() ,
,
将点![]() 分别代入,得:
分别代入,得:
![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为![]() ,
,
当x=﹣1时,y=![]() ,
,
∴所求点C的坐标为![]() .
.
(3)①当以OA为对角线时
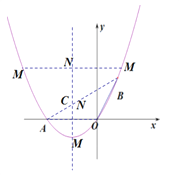
OA与MN互相垂直且平分
∴点M![]()
②当以OA为边时
OA=MN且OA//MN
即MN=2,MN//x轴
设N(-1,t)
则M(-3,t)或(1,t)
![]()
![]()
![]()
综上:点M的坐标为:![]() 、
、![]()


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】已知某服装厂现有![]() 种布料70米,
种布料70米,![]() 种布料52米,现计划用这两种布料生产
种布料52米,现计划用这两种布料生产![]() 、
、![]() 两种型号的时装共80套.已知做一套
两种型号的时装共80套.已知做一套![]() 型号的时装需用A种布料1.1米,
型号的时装需用A种布料1.1米,![]() 种布料0.4米,可获利50元;做一套
种布料0.4米,可获利50元;做一套![]() 型号的时装需用
型号的时装需用![]() 种布料0.6米,
种布料0.6米,![]() 种布料0.9米,可获利45元.设生产
种布料0.9米,可获利45元.设生产![]() 型号的时装套数为
型号的时装套数为![]() ,用这批布料生产两种型号的时装所获得的总利润为
,用这批布料生产两种型号的时装所获得的总利润为![]() 元.
元.
(1)求![]() (元)与
(元)与![]() (套)的函数关系式.
(套)的函数关系式.
(2)有几种生产方案?
(3)如何生产使该厂所获利润最大?最大利润是多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列动车从A地开往B地,一列普通列车从B地开往A地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示y与x之间的函数关系,下列说法中正确的是:( )
①AB两地相距1000千米;②两车出发后3小时相遇;③普通列车的速度是100千米/小时;④动车从A地到达B地的时间是4小时.
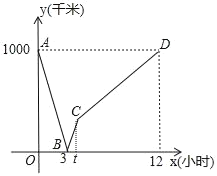
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=BC,D为AC中点,过点D作DE∥BC,交AB于点E.
(1)求证:AE=DE;
(2)若∠C=65°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣4x﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C,点P是抛物线上的一个不与点C重合的一个动点,若S△PAB=S△ABC,则点P的坐标是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点N(0,-1)的直线y=kx+b与图中的四边形ABCD有不少于两个交点,其中A(2,3)、B(1,1)、C(4,1)、D(4,3),则k的取值范围____________
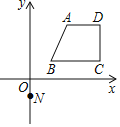
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,两锐角的度数之比为2:1,其最短边为1,射线CP交AB所在的直线于点P,且∠ACP=30°,则线段CP的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com