
【题目】如图,已知![]() 是
是![]() 的外接圆,
的外接圆,![]() ,
,![]() 是劣弧
是劣弧![]() 上的点(不与点
上的点(不与点![]() 、
、![]() 重合),延长
重合),延长![]() 至
至![]() .
.
![]() 求证:
求证:![]() 的延长线
的延长线![]() 平分
平分![]() ;
;
![]() 若
若![]() ,
,![]() 中
中![]() 边上的高为
边上的高为![]() ,求
,求![]() 的面积.
的面积.
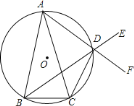
【答案】(1)见解析;(2)![]() 的外接圆的面积为
的外接圆的面积为![]() .
.
【解析】
(1)要证明AD的延长线平分∠CDE,即证明∠EDF=∠CDF,转化为证明∠ADB=∠CDF,再根据A,B,C,D四点共圆的性质,和等腰三角形角之间的关系即可得到.
(2)求△ABC外接圆的面积.只需解出圆半径,故作等腰三角形底边上的垂直平分线即过圆心,再连接OC,根据角之间的关系在三角形内即可求得圆半径,可得到外接圆面积.
![]() 证明:如图,设
证明:如图,设![]() 为
为![]() 延长线上一点,
延长线上一点,

∵![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆,
四点共圆,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() 的延长线平分
的延长线平分![]() .
.
![]() 设
设![]() 为外接圆圆心,连接
为外接圆圆心,连接![]() 比延长交
比延长交![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,

∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
设圆半径为![]() ,
,
则![]() ,
,
∵![]() 中
中![]() 边上的高为
边上的高为![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() 的外接圆的面积为:
的外接圆的面积为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,![]() ,且
,且![]() .
.
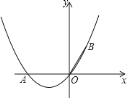
![]() 求经过
求经过![]() ,
,![]() ,
,![]() 三点的抛物线的解析式.
三点的抛物线的解析式.
![]() 在
在![]() 中抛物线的对称轴上是否存在点
中抛物线的对称轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 若点
若点![]() 为抛物线上一点,点
为抛物线上一点,点![]() 为对称轴上一点,是否存在点
为对称轴上一点,是否存在点![]() ,
,![]() 使得
使得![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形是平行四边形?若存在,求出点
构成的四边形是平行四边形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形的两条边的和是第三边的两倍,则称这个三角形是“优三角形”,这两条边的比称为“优比”(若这两边不等,则优比为较大边与较小边的比),记为![]() .
.
(1)命题:“等边三角形为优三角形,其优比为1”,是真命题还是假命题?
(2)已知![]() 为优三角形,
为优三角形,![]() ,
,![]() ,
,![]() ,
,
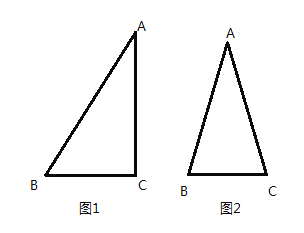
①如图1,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
②如图2,若![]() ,求优比
,求优比![]() 的取值范围.
的取值范围.
(3)已知![]() 是优三角形,且
是优三角形,且![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
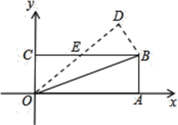
【题目】如图,在平面直角坐标系xOy中,O为坐标原点,A(4,0),B(4,2),C(0,2),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程![]() ,下列说法:①若
,下列说法:①若![]() ,则方程必有一根为
,则方程必有一根为![]() ;②若
;②若![]() 是方程
是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;③若
成立;③若![]() ,则方程
,则方程![]() 一定有两个不相等实数根;其中正确结论有( )个.
一定有两个不相等实数根;其中正确结论有( )个.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:
因式分解----“分组分解法”:分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式,比如,四项的多项式一般按照“两两”分组或“三一”分组进行分组分解.分析多项式的特点,恰当的分组是分组分解法的关键.
例1:“两两”分组:
![]()
![]()
![]()
![]()
我们把![]() 和
和![]() 两项分为一组,
两项分为一组,![]() 和
和![]() 两项分为一组,分别提公因式,立即解除了困难.同样.这道题也可以这样做:
两项分为一组,分别提公因式,立即解除了困难.同样.这道题也可以这样做:
![]()
![]()
![]()
![]()
例2:“三一”分组:
![]()
![]()
![]()
我们把![]() ,
,![]() ,
,![]() 三项分为一组,运用完全平方公式得到
三项分为一组,运用完全平方公式得到![]() ,再与-1用平方差公式分解,问题迎刃而解.
,再与-1用平方差公式分解,问题迎刃而解.
归纳总结:用分组分解法分解因式的方法是先恰当分组,然后用提公因式法或运用公式法继续分解.
请同学们在阅读材料的启发下,解答下列问题:
(1)分解因式:
①![]() ;
;
②![]()
(2)若多项式![]() 利用分组分解法可分解为
利用分组分解法可分解为![]() ,请写出
,请写出![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
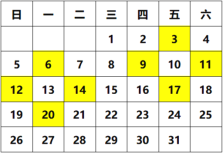
【题目】在日历上,我们可以发现其中某些数满足一定的规律,如图是2020年1月份的日历.如图所选择的两组四个数,分别将每组数中相对的两数相乘,再相减,例如:9×11﹣3×17= ,12×14﹣6×20= ,不难发现,结果都是 .
(1)请将上面三个空补充完整;
(2)请你利用整式的运算对以上规律进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校图书馆大楼工程在招标时,接到甲乙两个工程队的投标书,每施工一个月,需付甲工程队工程款16万元,付乙工程队12万元。工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:
(1)甲队单独完成此项工程刚好如期完工;
(2)乙队单独完成此项工程要比规定工期多用3个月;
(3)若甲乙两队合作2个月,剩下的工程由乙队独做也正好如期完工。
你觉得哪一种施工方案最节省工程款,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com