
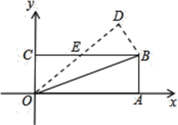
【题目】如图,在平面直角坐标系xOy中,O为坐标原点,A(4,0),B(4,2),C(0,2),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为_____.
【答案】![]()
【解析】
根据矩形的性质结合折叠的性质得出![]() ,进而可以得出
,进而可以得出![]() ,设点E的坐标为(m,1),则
,设点E的坐标为(m,1),则![]() ,CE=m,利用勾股定理即可求出m的值,在根据点E的坐标,利用待定系数法即可求出OD所在直线的解析式.
,CE=m,利用勾股定理即可求出m的值,在根据点E的坐标,利用待定系数法即可求出OD所在直线的解析式.
解::∵A(3,0),B(3,1),C(0,1),O(0,0),
∴四边形OABC为矩形,∴∠EBO=∠AOB.
又∵∠EOB=∠AOB,∴∠EOB=∠EBO,∴OE=BE.
设点E的坐标为(m,2),则OE=BE=4-m,CE=m,
在Rt△OCE中,OC=2,CE=m,OE=4-m,
∴![]() ∴m=
∴m=![]() ,
,
∴点E的坐标为(![]() ,2)
,2)
设OD所在直线的解析式为y=kx,
将E的坐标(![]() ,2)代入y=kx中,
,2)代入y=kx中,
得:![]() ,解得:
,解得:![]() ,
,
∴OD所在直线的解析式为![]()


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=BC,D为AC中点,过点D作DE∥BC,交AB于点E.
(1)求证:AE=DE;
(2)若∠C=65°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C2018,若点P(4035,m)在第2018段抛物线C2018上,则m的值是

A. 1 B. -1 C. 0 D. 4035
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点O为坐标原点,正方形OABC的边OA,OC分别在x轴,y轴上,点B的坐标为(4,4),反比例函数![]() 的图象经过线段BC的中点D,交正方形OABC的另一边AB于点E.
的图象经过线段BC的中点D,交正方形OABC的另一边AB于点E.
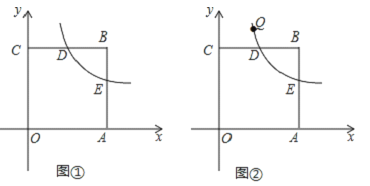
(1)求k的值;
(2)如图①,若点P是x轴上的动点,连接PE,PD,DE,当△DEP的周长最短时,求点P的坐标;
(3)如图②,若点Q(x,y)在该反比例函数图象上运动(不与D重合),过点Q作QM⊥y轴,垂足为M,作QN⊥BC所在直线,垂足为N,记四边形CMQN的面积为S,求S关于x的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
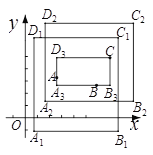
若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的外延矩形.点A,B,C的所有外延矩形中,面积最小的矩形称为点A,B,C的最佳外延矩形.例如,图中的矩形![]() ,
,![]() ,
,![]() 都是点A,B,C的外延矩形,矩形
都是点A,B,C的外延矩形,矩形![]() 是点A,B,C的最佳外延矩形.
是点A,B,C的最佳外延矩形.
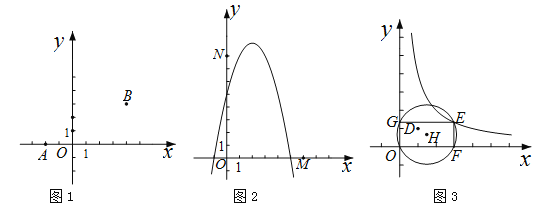
(1)如图1,已知A(-2,0),B(4,3),C(0,![]() ).
).
①若![]() ,则点A,B,C的最佳外延矩形的面积为 ;
,则点A,B,C的最佳外延矩形的面积为 ;
②若点A,B,C的最佳外延矩形的面积为24,则![]() 的值为 ;
的值为 ;
(2)如图2,已知点M(6,0),N(0,8).P(![]() ,
,![]() )是抛物线
)是抛物线![]() 上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标
上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标![]() 的取值范围;
的取值范围;
(3)如图3,已知点D(1,1).E(![]() ,
,![]() )是函数
)是函数![]() 的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.
的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.


查看答案和解析>>
科目:初中数学 来源: 题型:
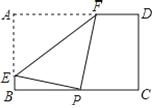
【题目】如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式: ![]() ;
;![]() ;
;![]() ;……
;……
根据上面等式反映的规律,解答下列问题:
(1)请根据上述等式的特征,在括号内填上同一个实数: ![]() ( )-5=( )
( )-5=( )![]() ;
;
(2)小明将上述等式的特征用字母表示为:![]() (
(![]() 、
、![]() 为任意实数).
为任意实数).
①小明和同学讨论后发现:![]() 、
、![]() 的取值范围不能是任意实数.请你直接写出
的取值范围不能是任意实数.请你直接写出![]() 、
、![]() 不能取哪些实数.
不能取哪些实数.
②是否存在![]() 、
、![]() 两个实数都是整数的情况?若存在,请求出
两个实数都是整数的情况?若存在,请求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com