
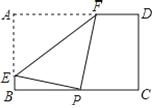
【题目】如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是_________________.
【答案】6-2![]() ≤x≤4.
≤x≤4.
【解析】试题分析:此题需要运用极端原理求解:①BP最小时,F、D重合,由折叠的性质知:AF=PF,在Rt△PFC中,利用勾股定理可求得PC的长,进而可求得BP的值,即BP的最小值;②BP最大时,E、B重合,根据折叠的性质即可得到AB=BP=34,即BP的最大值为4;根据上述两种情况即可得到BP的取值范围.
试题解析:如图:
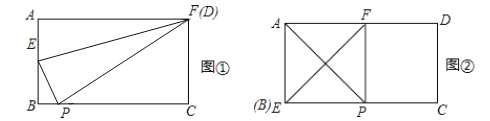
①当F、D重合时,BP的值最小;
根据折叠的性质知:AF=PF=6;
在Rt△PFC中,PF=6,FC=4,则PC=2![]() ;
;
∴BP=xmin=6-2![]() ;
;
②当E、B重合时,BP的值最大;根据折叠的性质即可得到AB=BP=4,即BP的最大值为4;
故答案为:6-2![]() ≤x≤4.
≤x≤4.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
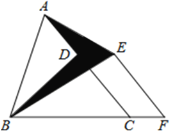
A.3B.4C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
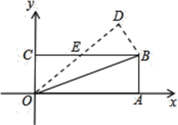
【题目】如图,在平面直角坐标系xOy中,O为坐标原点,A(4,0),B(4,2),C(0,2),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:
因式分解----“分组分解法”:分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式,比如,四项的多项式一般按照“两两”分组或“三一”分组进行分组分解.分析多项式的特点,恰当的分组是分组分解法的关键.
例1:“两两”分组:
![]()
![]()
![]()
![]()
我们把![]() 和
和![]() 两项分为一组,
两项分为一组,![]() 和
和![]() 两项分为一组,分别提公因式,立即解除了困难.同样.这道题也可以这样做:
两项分为一组,分别提公因式,立即解除了困难.同样.这道题也可以这样做:
![]()
![]()
![]()
![]()
例2:“三一”分组:
![]()
![]()
![]()
我们把![]() ,
,![]() ,
,![]() 三项分为一组,运用完全平方公式得到
三项分为一组,运用完全平方公式得到![]() ,再与-1用平方差公式分解,问题迎刃而解.
,再与-1用平方差公式分解,问题迎刃而解.
归纳总结:用分组分解法分解因式的方法是先恰当分组,然后用提公因式法或运用公式法继续分解.
请同学们在阅读材料的启发下,解答下列问题:
(1)分解因式:
①![]() ;
;
②![]()
(2)若多项式![]() 利用分组分解法可分解为
利用分组分解法可分解为![]() ,请写出
,请写出![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
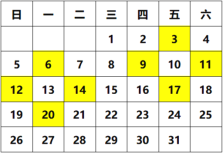
【题目】在日历上,我们可以发现其中某些数满足一定的规律,如图是2020年1月份的日历.如图所选择的两组四个数,分别将每组数中相对的两数相乘,再相减,例如:9×11﹣3×17= ,12×14﹣6×20= ,不难发现,结果都是 .
(1)请将上面三个空补充完整;
(2)请你利用整式的运算对以上规律进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
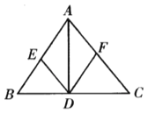
【题目】如图,已知:AD是△ABC的角平分线,DE//AC交AB于E,DF//AB交AC于F,
(1)求证:四边形AEDF是菱形;
(2)当△ABC满足什么条件时,四边形AEDF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
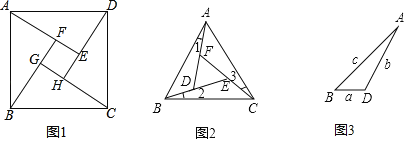
【题目】问题背景:如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得四边形EFGH是正方形.
类比探究:如图2,在正△ABC的内部,作∠1=∠2=∠3,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)如图3,进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
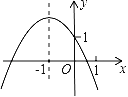
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a﹣b+c>1;③abc>0;④4a﹣2b+c<0;⑤c﹣a>1.其中所有正确结论的序号是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com