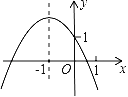
[题目]已知二次函数y=ax2+bx+c的图象如图所示.有以下结论:①a+b+c＜0,②a﹣b+c＞1,③abc＞0,④4a﹣2b+c＜0,⑤c﹣a＞1．其中所有正确结论的序号是．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】已知二次函数y=ax2+bx+c的图象如图所示，有以下结论：①a+b+c＜0；②a﹣b+c＞1；③abc＞0；④4a﹣2b+c＜0；⑤c﹣a＞1．其中所有正确结论的序号是_____．

【答案】①②③⑤

【解析】试题解析：①当x=1时，y=a+b+c<0，故①正确；

②当x=1时，y=ab+c>1，故②正确；

③由抛物线的开口向下知a<0，与y轴的交点为在y轴的正半轴上，

∴c>0,对称轴为得2a=b，

∴a、b同号，即b<0，

∴abc>0，故③正确；

④∵对称轴为

∴点(0,1)的对称点为(2,1)，

∴当x=2时，y=4a2b+c=1，故④错误；

⑤∵x=1时,ab+c>1,又即b=2a，

∴ca>1，故⑤正确.

故答案为：①②③⑤.

练习册系列答案

高考调研衡水重点中学同步精讲精练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

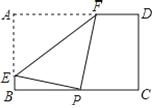
【题目】如图，矩形纸片ABCD中，AB=4，AD=6，点P是边BC上的动点，现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别为E、F，要使折痕始终与边AB、AD有交点，则BP的取值范围是_________________．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】观察下列等式：；；；……

根据上面等式反映的规律，解答下列问题：

（1）请根据上述等式的特征，在括号内填上同一个实数：（）-5=（）；

（2）小明将上述等式的特征用字母表示为：（、为任意实数）.

①小明和同学讨论后发现：、的取值范围不能是任意实数.请你直接写出、不能取哪些实数.

②是否存在、两个实数都是整数的情况？若存在，请求出、的值；若不存在，请说明理由.

查看答案和解析>>

科目：初中数学 来源： 题型：

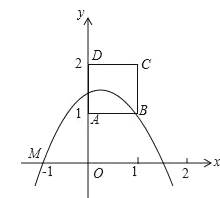
【题目】如图，边长为1的正方形ABCD顶点A（0，1），B（1，1）；一抛物线y=ax2+bx+c过点M（﹣1，0）且顶点在正方形ABCD内部（包括在正方形的边上），则a的取值范围是（　　）

A. ﹣2≤a≤﹣1 B. ﹣2≤a≤﹣ C. ﹣1≤a≤﹣ D. ﹣1≤a≤﹣

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在学习了一次函数图像后,张明、李丽和王林三位同学在赵老师的指导下,对一次函数进行了探究学习,请根据他们的对话解答问题.

(1)张明:当时,我能求出直线与轴的交点坐标为 ;

李丽:当时,我能求出直线与坐标轴围成的三角形的面积为 ;

(2)王林:根据你们的探究,我发现无论取何值,直线总是经过一个固定的点,请求出这个定点的坐标.

(3)赵老师:我来考考你们,如果点的坐标为,该点到直线的距离存在最大值吗?若存在,试求出该最大值;若不存在,请说明理由.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某商家销售一款商品，进价每件80元，售价每件145元，每天销售40件，每销售一件需支付给商场管理费5元，未来一个月按30天计算，这款商品将开展“每天降价1元”的促销活动，即从第一天开始每天的单价均比前一天降低1元，通过市场调查发现，该商品单价每降1元，每天销售量增加2件，设第x天且x为整数的销售量为y件．