
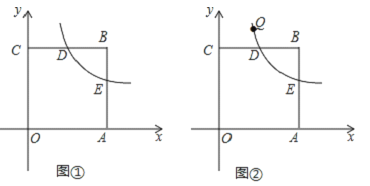
【题目】如图,在平面直角坐标系xOy中,点O为坐标原点,正方形OABC的边OA,OC分别在x轴,y轴上,点B的坐标为(4,4),反比例函数![]() 的图象经过线段BC的中点D,交正方形OABC的另一边AB于点E.
的图象经过线段BC的中点D,交正方形OABC的另一边AB于点E.
(1)求k的值;
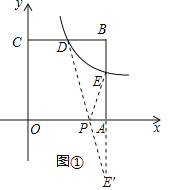
(2)如图①,若点P是x轴上的动点,连接PE,PD,DE,当△DEP的周长最短时,求点P的坐标;
(3)如图②,若点Q(x,y)在该反比例函数图象上运动(不与D重合),过点Q作QM⊥y轴,垂足为M,作QN⊥BC所在直线,垂足为N,记四边形CMQN的面积为S,求S关于x的函数关系式,并写出x的取值范围.
【答案】(1)8 ;(2)(![]() );(3)S=8-4x,0<x<2;S=4x-8,x>2
);(3)S=8-4x,0<x<2;S=4x-8,x>2
【解析】
(1)首先根据题意求出C点的坐标,然后根据中点坐标公式求出D点坐标,由反比例函数y=![]() (x>0,k≠0)的图象经过线段BC的中点D,D点坐标代入解析式求出k即可;
(x>0,k≠0)的图象经过线段BC的中点D,D点坐标代入解析式求出k即可;
(2)根据轴对称的性质找到点P的位置:作点E关于x轴的对称点E′,连接DE′,交x轴于点P,求得直线DE′与x轴的交点坐标即可;
(3)分两步进行解答,①当Q在直线BC的上方时,即0<x<2,如图1,根据S四边形CMQN=CNQD列出S关于x的解析式,②当Q在直线BC的下方时,即x>2,如图2,依然根据S四边形CMQN=CNQD列出S关于x的解析式.
(1)如图①,
∵正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(4,4),
∴C(0,4),
∵D是BC的中点,
∴D(2,4),
∵反比例函数y=![]() (x>0,k≠0)的图象经过点D,
(x>0,k≠0)的图象经过点D,
∴k=8;
(2)如图①,作点E关于x轴的对称点E′,连接DE′,交x轴于点P,
把x=4代入y=![]() ,得y=2,则E(4,2),
,得y=2,则E(4,2),
故点E关于x轴对称的点E′(4,-2),
设直线DE′的方程为y=kx+b(k≠0),
将D(2,4),E′(4,-2)分别代入得到:![]() ,
,
解得![]() ,
,
故直线DE′的方程为y=-3x+10,
当y=0时,x=![]() ,
,
即P(![]() ,0);
,0);
(3)如图②,
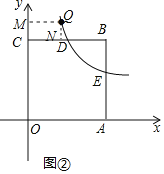
当Q在直线BC的上方时,即0<x<2,
如图1,∵点Q(x,y)在该反比例函数的图象上运动,
∴y=![]() ,
,
∴S四边形CMQN=CNQD=x(![]() -4)=8-4x(0<x<2),
-4)=8-4x(0<x<2),
如图③,
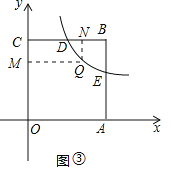
当Q在直线BC的下方时,即x>4,同理求出S四边形CMQN=CNQD=x(4-![]() )=4x-8(x>2),
)=4x-8(x>2),
综上S=![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:初中数学 来源: 题型:
【题目】某中学七、八年级各选![]() 名同学参加“创全国文明城市”知识竞赛,计分
名同学参加“创全国文明城市”知识竞赛,计分![]() 分制,选手得分均为整数,成绩达到
分制,选手得分均为整数,成绩达到![]() 分或
分或![]() 分以上为合格,达到
分以上为合格,达到![]() 分或
分或![]() 分以上为优秀,这次竞赛后,七、八年级两支代表队成绩分布的条形统计图和成绩分析表如下,其中七年级代表队得
分以上为优秀,这次竞赛后,七、八年级两支代表队成绩分布的条形统计图和成绩分析表如下,其中七年级代表队得![]() 分、
分、![]() 分选手人数分别为
分选手人数分别为![]() ,
,![]() .
.
队列 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
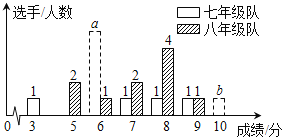
(1)根据图表中的数据,求![]() ,
,![]() 的值.
的值.
(2)直接写出表中的![]() ,
,![]() .
.
(3)你是八年级学生,请你给出两条支持八年级队成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
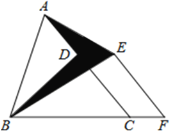
A.3B.4C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
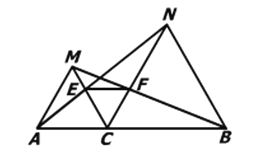
【题目】如图,点C为线段AB上一点,△ACM, △CBN是等边三角形,连结AN,交MC于点E,连结MB交CN于F.
(1)求证:AN=BM;
(2)求证: ∠CEA=∠CFM .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形的两条边的和是第三边的两倍,则称这个三角形是“优三角形”,这两条边的比称为“优比”(若这两边不等,则优比为较大边与较小边的比),记为![]() .
.
(1)命题:“等边三角形为优三角形,其优比为1”,是真命题还是假命题?
(2)已知![]() 为优三角形,
为优三角形,![]() ,
,![]() ,
,![]() ,
,
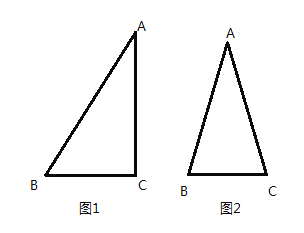
①如图1,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
②如图2,若![]() ,求优比
,求优比![]() 的取值范围.
的取值范围.
(3)已知![]() 是优三角形,且
是优三角形,且![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
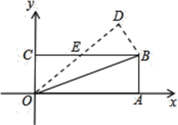
【题目】如图,在平面直角坐标系xOy中,O为坐标原点,A(4,0),B(4,2),C(0,2),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:
因式分解----“分组分解法”:分组分解法指通过分组分解的方式来分解用提公因式法和公式法无法直接分解的多项式,比如,四项的多项式一般按照“两两”分组或“三一”分组进行分组分解.分析多项式的特点,恰当的分组是分组分解法的关键.
例1:“两两”分组:
![]()
![]()
![]()
![]()
我们把![]() 和
和![]() 两项分为一组,
两项分为一组,![]() 和
和![]() 两项分为一组,分别提公因式,立即解除了困难.同样.这道题也可以这样做:
两项分为一组,分别提公因式,立即解除了困难.同样.这道题也可以这样做:
![]()
![]()
![]()
![]()
例2:“三一”分组:
![]()
![]()
![]()
我们把![]() ,
,![]() ,
,![]() 三项分为一组,运用完全平方公式得到
三项分为一组,运用完全平方公式得到![]() ,再与-1用平方差公式分解,问题迎刃而解.
,再与-1用平方差公式分解,问题迎刃而解.
归纳总结:用分组分解法分解因式的方法是先恰当分组,然后用提公因式法或运用公式法继续分解.
请同学们在阅读材料的启发下,解答下列问题:
(1)分解因式:
①![]() ;
;
②![]()
(2)若多项式![]() 利用分组分解法可分解为
利用分组分解法可分解为![]() ,请写出
,请写出![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
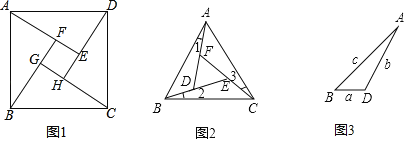
【题目】问题背景:如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得四边形EFGH是正方形.
类比探究:如图2,在正△ABC的内部,作∠1=∠2=∠3,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)如图3,进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com