
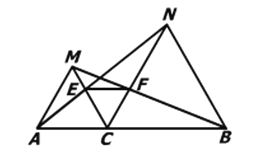
【题目】如图,点C为线段AB上一点,△ACM, △CBN是等边三角形,连结AN,交MC于点E,连结MB交CN于F.
(1)求证:AN=BM;
(2)求证: ∠CEA=∠CFM .
【答案】(1)见详解;(2)见详解.
【解析】
(1)由等边三角形可得其对应线段相等,对应角相等,进而可由SAS得到△ACN≌△MCB,结论得证;
(2)由(1)得△ACN≌△MCB,则∠CBF=∠CNE,由三角形的外角性质,即可得到∠CEA=∠CFM .
证明:如图:
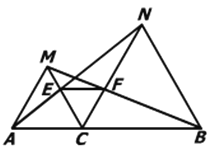
(1)∵△ACM,△CBN是等边三角形,
∴AC=MC,CN=CB,,∠ACM=∠NCB=60°,
∴∠ACM+∠MCN=∠NCB+∠MCN,
即∠ACN=∠MCB,
在△ACN和△MCB中,
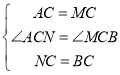 ,
,
∴△ACN≌△MCB(SAS),
∴AN=BM.
(2)由(1)得,△ACN≌△MCB,
∴∠CBF=∠CNE,
∵∠ACM=∠NCB=∠MCN=60°,
∴∠CBF+∠NCB=∠CNE+∠MCN,
∴∠CEA=∠CFM .


科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C2018,若点P(4035,m)在第2018段抛物线C2018上,则m的值是

A. 1 B. -1 C. 0 D. 4035
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与直线y=x+3分别交于x轴和y轴上同一点,交点分别是点A和点C,且抛物线的对称轴为x=﹣2.
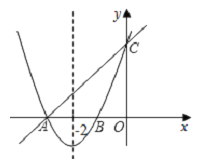
(1)求出抛物线与x轴的两个交点A、B的坐标.
(2)求出该抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点O为坐标原点,正方形OABC的边OA,OC分别在x轴,y轴上,点B的坐标为(4,4),反比例函数![]() 的图象经过线段BC的中点D,交正方形OABC的另一边AB于点E.
的图象经过线段BC的中点D,交正方形OABC的另一边AB于点E.
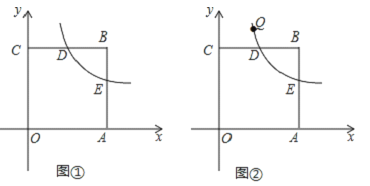
(1)求k的值;
(2)如图①,若点P是x轴上的动点,连接PE,PD,DE,当△DEP的周长最短时,求点P的坐标;
(3)如图②,若点Q(x,y)在该反比例函数图象上运动(不与D重合),过点Q作QM⊥y轴,垂足为M,作QN⊥BC所在直线,垂足为N,记四边形CMQN的面积为S,求S关于x的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
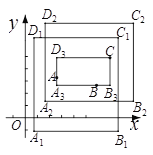
若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的外延矩形.点A,B,C的所有外延矩形中,面积最小的矩形称为点A,B,C的最佳外延矩形.例如,图中的矩形![]() ,
,![]() ,
,![]() 都是点A,B,C的外延矩形,矩形
都是点A,B,C的外延矩形,矩形![]() 是点A,B,C的最佳外延矩形.
是点A,B,C的最佳外延矩形.
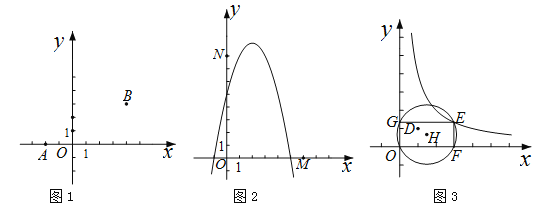
(1)如图1,已知A(-2,0),B(4,3),C(0,![]() ).
).
①若![]() ,则点A,B,C的最佳外延矩形的面积为 ;
,则点A,B,C的最佳外延矩形的面积为 ;
②若点A,B,C的最佳外延矩形的面积为24,则![]() 的值为 ;
的值为 ;
(2)如图2,已知点M(6,0),N(0,8).P(![]() ,
,![]() )是抛物线
)是抛物线![]() 上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标
上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标![]() 的取值范围;
的取值范围;
(3)如图3,已知点D(1,1).E(![]() ,
,![]() )是函数
)是函数![]() 的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.
的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com