Question

【题目】如图，AB是⊙O的直径，BC为⊙O的切线，切点为B，OC平行于AD，OA=2．

（1）求证：CD是⊙O的切线；
（2）若AD+OC=9，求CD的长．（结果保留根号）

Answer 1

【答案】
（1）证明：连结OD．

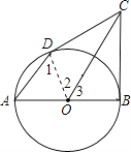
∵AD∥OC，

∴∠1=∠2，∠A=∠3．

∵OA=OD，

∴∠A=∠1，

∴∠2=∠3，

∴在△ODC与△OBC中，

，

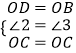∴△ODC≌△OBC（SAS），

∴∠ODC=∠OBC=90°，即OD⊥CD．

又OD是圆O的半径，

∴CD是⊙O的切线

（2）证明：连结BD，

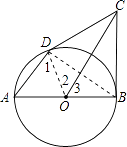
∵AB为⊙O的直径，∴∠ADB=90°，

∵∠OBC=90°，∴∠ADB=∠OBC

又∠A=∠3，∴△ADB∽△OBC

∴ ，ADOC=OBAB=2×4=8；

又AD+OC=9，

∴AD、OC是关于x的方程x2﹣9x+8=0的两个根．

∵OC＞OD，∴OC=8，AD=1，OD=2，

∴CD=

【解析】（1）如图，连接OD，欲证明CD是⊙O的切线，只需证得∠ODC=90°，即OD⊥CD即可；（2）由△ADB∽△OBC的对应边成比例求得ADOC=OBAB=2×4=8，结合已知条件“AD+OC=9”，则AD、OC是关于x的方程x2﹣9x+8=0的两个根．据此求得OC、OD的值，所以在直角△OCD中，根据勾股定理来求线段CD的长度即可．
【考点精析】掌握勾股定理的概念和切线的判定定理是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线．