
 如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为( )
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为( )| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
 如图,
如图,| 22+42 |
| 5 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| AB |
| AD |
| 1 |
| 2 |
| DH |
| OH |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| DH |
| EH |
| 3 |
| 4 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
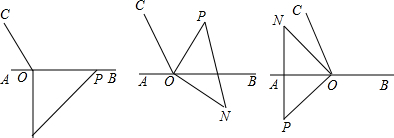
查看答案和解析>>
科目:初中数学 来源: 题型:
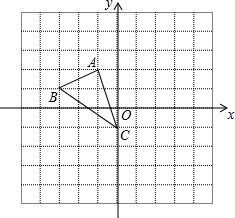 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1),
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1),查看答案和解析>>
科目:初中数学 来源: 题型:
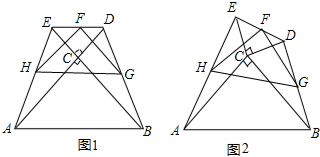
查看答案和解析>>
科目:初中数学 来源: 题型:
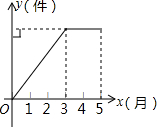 烈山留园存村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )
烈山留园存村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )| A、1月至3月每月生产总量逐月增加,4,5两月停止生产 |
| B、1月至3月每月生产总量不变,4,5两月均停止生产 |
| C、1月至3月每月生产总量逐月增加,4,5两月每月生产总量逐月减少 |
| D、1月至3月每月生产总量逐月增加,4,5两月生产量与3月持平 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com