
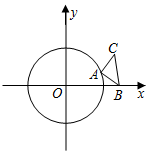
 如图,⊙O的半径为1,等腰直角三角形ABC的顶点B固定且坐标为($\sqrt{2}$,0),顶点A在⊙O上运动,始终保持∠CAB=90°,AC=AB
如图,⊙O的半径为1,等腰直角三角形ABC的顶点B固定且坐标为($\sqrt{2}$,0),顶点A在⊙O上运动,始终保持∠CAB=90°,AC=AB分析 (1)中有两种情况,即A点坐标为(1,0)或(-1,0),根据AB=AC,求出C点坐标;
(2)根据题意过点O作OM⊥BC于点M,求出OM的长,与半径比较得出位置关系;
(3)过点A作AE⊥OB于点E,在Rt△OAE中求AE的长,然后再在Rt△BAE中求出AB的长,进而求出面积的表达式,根据自变量的取值范围确定最大最小值;
(4)相切时有两种情况,在第一象限或者第四象限,连接OA,并过点A作AE⊥OB于点E,在Rt△OAE中求出OE,然后就能求出A点坐标,AB所在直线对应的函数关系式很容易就能求出.
解答 解:
(1)当点A的坐标为(1,0)时,AB=AC=$\sqrt{2}$-1,点C的坐标为(1,$\sqrt{2}$-1)或(1,1-$\sqrt{2}$);
当点A的坐标为(-1,0)时,AB=AC=$\sqrt{2}$+1,点C的坐标为(-1,$\sqrt{2}$+1)或(-1,-$\sqrt{2}$-1);
(2)直线BC与⊙O相切.
如图1,过点O作OM⊥BC于点M,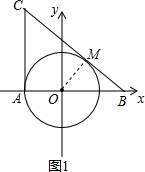
∴∠OBM=∠BOM=45°,
∴OM=OB•sin45°=1
∴直线BC与⊙O相切;
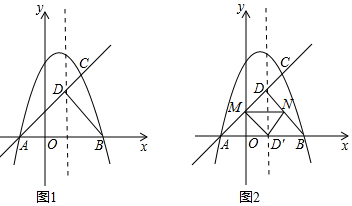
(3)过点A作AE⊥OB于点E,如图2,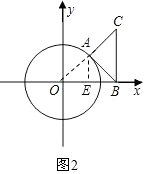
在Rt△OAE中,AE2=OA2-OE2=1-x2,
在Rt△BAE中,AB2=AE2+BE2=(1-x2)+($\sqrt{2}$-x)2=3-2$\sqrt{2}$x
∴S=$\frac{1}{2}$AB•AC=$\frac{1}{2}$AB2=$\frac{1}{2}$(3-2$\sqrt{2}$x)=$\frac{3}{2}$-$\sqrt{2}$x,
其中-1≤x≤1,
当x=-1时,S的最大值为$\frac{3}{2}$+$\sqrt{2}$,
当x=1时,S的最小值为$\frac{3}{2}$-$\sqrt{2}$;
(4)①当点A位于第一象限时(如右图3):
连接OA,并过点A作AE⊥OB于点E,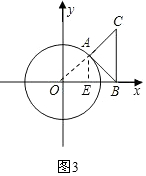
∵直线AB与⊙O相切,
∴∠OAB=90°,
又∵∠CAB=90°,
∴∠CAB+∠OAB=180°,
∴点O、A、C在同一条直线
∴∠AOB=∠C=45°,即∠CBO=90°,
在Rt△OAE中,OE=AE=$\frac{\sqrt{2}}{2}$,
点A的坐标为($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)
过A、B两点的直线为y=-x+$\sqrt{2}$;
②当点A位于第四象限时(如图4),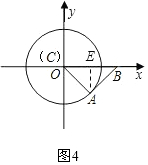
点A的坐标为($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$)
∵B的坐标为($\sqrt{2}$,0)
∴过A、B两点的直线为y=x-$\sqrt{2}$.
点评 本题为圆的综合应用,涉及切线的性质与判定、直线与圆的位置关系、等腰直角三角形的性质以及待定系数法求一次函数解析式等知识.此题难度较大,注意掌握辅助线的作法,注意掌握方程思想、分类讨论思想与数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 1或-1 | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com