
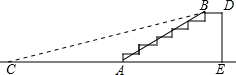
 如图,某公园入口原有一段台阶,其倾角∠BAE=30°,高DE=2m,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是(10-2$\sqrt{3}$)m.
如图,某公园入口原有一段台阶,其倾角∠BAE=30°,高DE=2m,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是(10-2$\sqrt{3}$)m. 分析 过点B作BF⊥CE于点F,分别根据∠BAE=30°,斜坡BC的坡度i=1:5,在Rt△ABF和Rt△BCF中求出AF、CF的长度,然后求出AC的长度.
解答 解:如图,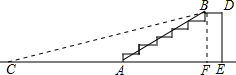 过点B作BF⊥CE于点F,
过点B作BF⊥CE于点F,
则BF=DE=2m,
在Rt△ABF中,
∵∠BAE=30°,
∴AF=$\frac{BF}{tan30°}$=$\frac{2}{\frac{\sqrt{3}}{3}}$=2$\sqrt{3}$(m),
在Rt△BCF中,
∵BF:CF=1:5,
∴CF=5×2=10,
则AC=CF-AF=(10-2$\sqrt{3}$)m.
故答案为:(10-2$\sqrt{3}$)m.
点评 本题考查了坡度及坡角的知识,解答本题的关键是构造直角三角形,利用三角函数的知识求解,注意理解坡度与坡角的定义.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m、n)表示第m排从左向右第n个数,则(6,5)与(13,6)表示的两数之积是( )
将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按如图方式排列,若规定(m、n)表示第m排从左向右第n个数,则(6,5)与(13,6)表示的两数之积是( )| A. | $\sqrt{6}$ | B. | 6 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )
如图,已知a∥b,将一块三角尺放在这两条直线之间,使直角顶点在直线a上,较小的锐角的顶点在直线b上.若∠1=25°,则∠2的度数为( )| A. | 25° | B. | 35° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{400}{x-20}$=$\frac{320}{x}$ | B. | $\frac{400}{x+20}$=$\frac{320}{x}$ | C. | $\frac{400}{x}$+20=$\frac{320}{x}$ | D. | $\frac{400}{x}$=$\frac{320}{x+20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
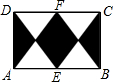 如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )
如图,一个矩形区域ABCD,点E、F分别是AB、DC的中点,则一只蝴蝶落在阴影部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{17}{38}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com