
分析 首先根据a1=-1,可得a2=$\frac{1}{1{-a}_{1}}$=$\frac{1}{1-(-1)}=\frac{1}{2}$,a3=$\frac{1}{1{-a}_{2}}$=$\frac{1}{1-\frac{1}{2}}=2$,${a}_{4}=\frac{1}{1-2}=-1$,…,所以这列数是-1、$\frac{1}{2}、2、-1、\frac{1}{2}、2$…,每3个数是一个循环;然后用2015除以3,求出一共有多少个循环,还剩下几个数,进而用循环的个数乘以$-1+\frac{1}{2}+2$,再加上剩下的数,求出a1+a2+a3+…+a2015的值是多少即可.
解答 解:因为a1=-1,
所以a2=$\frac{1}{1{-a}_{1}}$=$\frac{1}{1-(-1)}=\frac{1}{2}$,a3=$\frac{1}{1{-a}_{2}}$=$\frac{1}{1-\frac{1}{2}}=2$,${a}_{4}=\frac{1}{1-2}=-1$,…,
所以这列数是-1、$\frac{1}{2}、2、-1、\frac{1}{2}、2$…,
因为2015÷3=671…2,
所以a1+a2+a3+…+a2015
=671×($-1+\frac{1}{2}+2$)$+(-1+\frac{1}{2})$
=671×1.5-0.5
=1006.5-0.5
=1006
故答案为:1006.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:这列数是-1、$\frac{1}{2}、2、-1、\frac{1}{2}、2$…,每3个数是一个循环.


科目:初中数学 来源: 题型:选择题
| A. | 9.7×10-7 | B. | 97×10-7 | C. | 0.97×10-7 | D. | 9.7×10-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
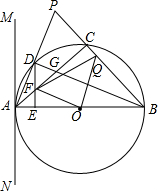 如图,已知△ABP是等腰三角形,AB=BP,以AB为直径的⊙O交AP于点D,交BP于点C,连接BD交AC于点G,直线MN过点A,且∠PAM=$\frac{1}{2}$∠ABP.
如图,已知△ABP是等腰三角形,AB=BP,以AB为直径的⊙O交AP于点D,交BP于点C,连接BD交AC于点G,直线MN过点A,且∠PAM=$\frac{1}{2}$∠ABP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
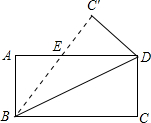 如图,将长方形纸片ABCD沿对角线BD折叠,使点C落在C′处,BC′交AD于E.若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有( )
如图,将长方形纸片ABCD沿对角线BD折叠,使点C落在C′处,BC′交AD于E.若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
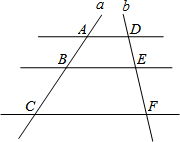 如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F,若AB=2,AC=6,DE=1.5,则DF的长为( )
如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F,若AB=2,AC=6,DE=1.5,则DF的长为( )| A. | 7.5 | B. | 6 | C. | 4.5 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
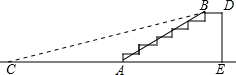 如图,某公园入口原有一段台阶,其倾角∠BAE=30°,高DE=2m,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是(10-2$\sqrt{3}$)m.
如图,某公园入口原有一段台阶,其倾角∠BAE=30°,高DE=2m,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是(10-2$\sqrt{3}$)m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com