
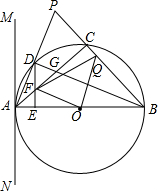
 如图,已知△ABP是等腰三角形,AB=BP,以AB为直径的⊙O交AP于点D,交BP于点C,连接BD交AC于点G,直线MN过点A,且∠PAM=$\frac{1}{2}$∠ABP.
如图,已知△ABP是等腰三角形,AB=BP,以AB为直径的⊙O交AP于点D,交BP于点C,连接BD交AC于点G,直线MN过点A,且∠PAM=$\frac{1}{2}$∠ABP.分析 (1)根据圆周角定理得到∠ADB=90°,而BA=BP,根据等腰三角形的性质得∠ABD=$\frac{1}{2}$∠ABP,加上∠PAM=$\frac{1}{2}$∠ABP,所以∠PAM=∠ABD,则利用∠ABD+∠BAD=90°可得∠PAM+∠BAD=90°,于是根据切线的判定定理可得直线MN是⊙O的切线;
(2)先利用等角的余角相等得到∠BDE=∠DAE,再利用三角形外角性质得∠AGD=∠GBA+∠GAB,然后利用等量代换可得∠AGD=∠DAC+∠GAB=∠DAE,于是有∠BDE=∠AGD,根据等腰三角形的判定即可得到△DFG是等腰三角形;
(3)延长QO到点K,使OK=OQ,如图,先证明FO垂直平分QK得到FK=FQ,再证明△OBQ≌△OAK得到BQ=AK,∠OBQ=∠OAK,接着根据圆周角定理得到∠ACB=90°,即∠CAB+∠ABC=90°,易得∠CAB+∠OAK=90°,即∠FAK=90°,然后在Rt△AFK中,根据勾股定理得到FK2=AF2+AK2,再利用等线段代换即可得到结论.
解答 (1)解:∵AB为直径,
∴∠ADB=90°,
∴BD⊥AP,
∵BA=BP,
∴BD平分∠ABP,即∠ABD=$\frac{1}{2}$∠ABP,
∵∠PAM=$\frac{1}{2}$∠ABP,
∴∠PAM=∠ABD,
∵∠ABD+∠BAD=90°,
∴∠PAM+∠BAD=90°,即∠BAM=90°,
∴AB⊥MN,
∴直线MN是⊙O的切线;
(2)证明:∵DE⊥AB,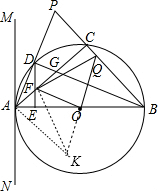
∴∠BDE+∠DBE=90°,
而∠DBA+∠DAB=90°,
∴∠BDE=∠DAE,
∵∠AGD=∠GBA+∠GAB
而∠GBA=∠DBC=∠DAC,
∴∠AGD=∠DAC+∠GAB=∠DAE,
∴∠BDE=∠AGD,
∴△DFG是等腰三角形;
(3)延长QO到点K,使OK=OQ,如图,
∵OQ⊥OF,OQ=OK,即FO垂直平分QK,
∴FK=FQ,
在△OBQ和△OAK中,
$\left\{\begin{array}{l}{OQ=OK}\\{∠BOQ=∠AOK}\\{OB=OA}\end{array}\right.$,
∴△OBQ≌△OAK,
∴BQ=AK,∠OBQ=∠OAK,
∵AB为直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
∴∠CAB+∠OAK=90°,即∠FAK=90°,
在Rt△AFK中,FK2=AF2+AK2,
∴FQ2=AF2+BQ2.
点评 本题考查了圆的综合题:熟练掌握圆周角定理、切线的判定定理和等腰三角形的判定与性质;会运用三角形全等证明角或线段相等;记住勾股定理.


科目:初中数学 来源: 题型:解答题
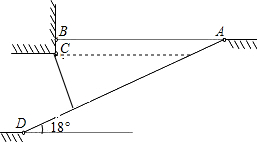 为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m)
为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com