
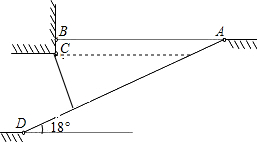
 为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m)
为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m)科目:初中数学 来源: 题型:选择题
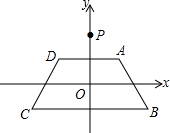 如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,则点P2014的坐标是( )
如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,则点P2014的坐标是( )| A. | (2014,2) | B. | (2014,-2) | C. | (2012,-2) | D. | (2012,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.7×10-7 | B. | 97×10-7 | C. | 0.97×10-7 | D. | 9.7×10-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
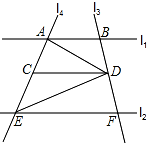 直线l1∥l2,直线l3与l1,l2,分别交于点B,F,直线l4与l1,l2分别交于点A,E,点D是直线l3上一动点,DC∥AB交l4于点C.
直线l1∥l2,直线l3与l1,l2,分别交于点B,F,直线l4与l1,l2分别交于点A,E,点D是直线l3上一动点,DC∥AB交l4于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
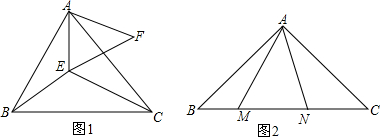
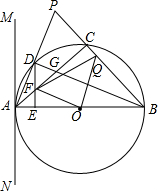 如图,已知△ABP是等腰三角形,AB=BP,以AB为直径的⊙O交AP于点D,交BP于点C,连接BD交AC于点G,直线MN过点A,且∠PAM=$\frac{1}{2}$∠ABP.
如图,已知△ABP是等腰三角形,AB=BP,以AB为直径的⊙O交AP于点D,交BP于点C,连接BD交AC于点G,直线MN过点A,且∠PAM=$\frac{1}{2}$∠ABP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com