
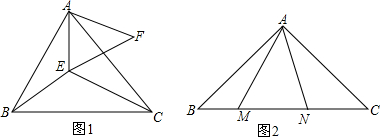
分析 (1)连接FC,根据等边三角形的性质得出AE=AF=EF=3,AB=AC,∠AFE=60°,∠BAC=∠EAF=60°,求出∠BAE=∠CAF,证出△BAE≌△CAF,推出CF=BE=4,∠AEB=∠AFC,求出CE2=EF2+CF2,推出∠CFE=90°即可;
(2)将△ABM绕A点逆时钟选择90,得到△AFC,则AM=AF,CF=BM,∠BAM=∠CAF,∠B=∠ACF,求出∠NAF=∠MAN,证△MAN≌△FAN,推出MN=FN,求出∠FCN=90°,
由勾股定理得出NF2=CF2+CN2即可.
解答 (1)解:
连接FC,
∵△ABC和△AEF为等边三角形,
∴AE=AF=EF=3,AB=AC,∠AFE=60°,∠BAC=∠EAF=60°,
∴∠BAE=∠CAF=60°-∠CAE,
在△BAE和△CAF中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAF}\\{AE=AF}\end{array}\right.$
∴△BAE≌△CAF,
∴CF=BE=4,∠AEB=∠AFC,
∴EF=3,CE=5,
∴CE2=EF2+CF2,
∴∠CFE=90°
∵∠AFE=60°,
∴∠AFC=90°+60°=150°,
∴∠AEB=∠AFC=150°;
(2)MN2=NC2+BM2,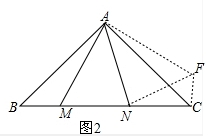
证明:将△ABM绕A点逆时钟选择90,得到△AFC,
则AM=AF,CF=BM,∠BAM=∠CAF,∠B=∠ACF,
∵∠BAC=90°,∠MAN=45°,
∴∠NAF=∠CAN+∠FAC=∠CAN+∠BAM=90°-45°=45°=∠MAN,
在△MAN和△FAN中
$\left\{\begin{array}{l}{AM=AF}\\{∠MAN=∠FAN}\\{AN=AN}\end{array}\right.$
∴△MAN≌△FAN,
∴MN=FN,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∵∠B=∠ACF,
∴∠ACF=45°,
∴∠FCN=90°,
由勾股定理得:NF2=CF2+CN2,
∵CF=BM,NF=MN,
∴MN2=NC2+BM2.
点评 本题考查了旋转的性质,全等三角形的性质和判定,勾股定理,勾股定理的逆定理,等边三角形的性质的应用,能综合运用定理进行推理是解此题的关键,有一定的难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
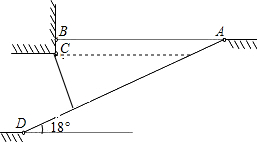 为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m)
为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
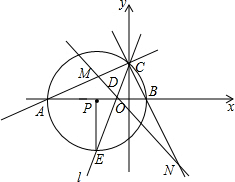 在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的⊙P过点C,若C的坐标为(0,2),AB=5,经过A、B、C三点的抛物线为y=ax2+bx+c.
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的⊙P过点C,若C的坐标为(0,2),AB=5,经过A、B、C三点的抛物线为y=ax2+bx+c.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.25°=900″ | B. | 1.5°=90′ | C. | 1000″=($\frac{5}{18}$)° | D. | 125.45°=1254.5′ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com