
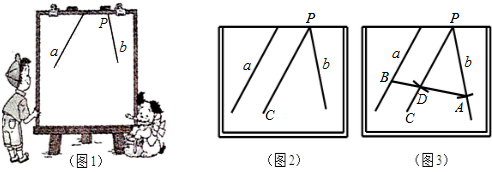
分析 (1)方法一:利用平行线的性质;方法二:利用三角形内角和定理;
(2)首先作等腰三角形△PBD,然后延长BD交直线a于点A,则四边形ABPQ就是所求作的图形.作图依据是等腰三角形的性质与平行线的性质;
(3)作出线段AB的垂直平分线EF,由等腰三角形的性质可知,EF是顶角的平分线,故EF即为所求作的图形.
解答 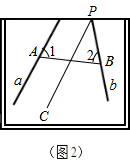 解:(1)方法一:
解:(1)方法一:
①如图2,画PC∥a,量出直线b与PC的夹角度数,
即为直线a,b所成角的度数,
②依据:两直线平行,同位角相等,
方法二:
①如图2,在直线a,b上各取一点A,B,连接AB,测得∠1、∠2的度数,
则180°-∠1-∠2即为直线a,b所成角的度数;
②依据:三角形内角和为180°;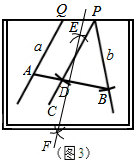
(2)①如图3,画PC∥a,以P为圆心,任意长为半径画弧,分别交直线b、PC于点B、D,连接BD并延长交直线a于点A,则四边形ABPQ就是所求等腰三角形在画板内的部分;作线段AB的垂直平分线EF,则EF就是所求作的线;
②∵a∥c,直线a与直线l所成的钝角为130°,
∴直线c与直线l所成的锐角为50°,
∴直线c与l所成的钝角为130°.
点评 本题涉及到的几何基本作图包括:(1)过直线外一点作直线的平行线,(2)作线段的垂直平分线;涉及到的考点包括:(1)平行线的性质;(2)等腰三角形的性质;(3)三角形内角和定理;(4)垂直平分线的性质等.本题借助实际问题场景考查了学生的几何基本作图能力,是一道好题.题目篇幅较长,需要仔细阅读,理解题意,正确作答.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
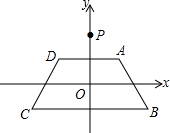 如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,则点P2014的坐标是( )
如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,则点P2014的坐标是( )| A. | (2014,2) | B. | (2014,-2) | C. | (2012,-2) | D. | (2012,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
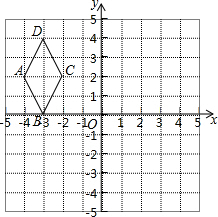 下面方格中有一个菱形ABCD和点O,请你在方格中画出以下图形(只要求画出平移、旋转后的图形,不要求写出作图步骤和过程).
下面方格中有一个菱形ABCD和点O,请你在方格中画出以下图形(只要求画出平移、旋转后的图形,不要求写出作图步骤和过程).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
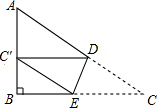 如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边的C′处,并且C′D∥BC,则CD的长是$\frac{40}{9}$.
如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边的C′处,并且C′D∥BC,则CD的长是$\frac{40}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com