练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．某电信公司手机的某类收费标准如下：不管通话的时间多长，每部手机每月必须缴月租费15元，另外，通话交费按0.15元/min计．
    （1）写出每月缴费y（元）与通话时间x（min）之间的关系式；
    （2）某手机用户这个月通话时间为120min，他应缴获费多少元？

    分析 （1）根据题意可以得出y=15+0.15x；
    （2）把x=120代入求出即可．

    解答 解：（1）y=15+0.15x；

    （2）当x=120时，y=15+0.15×120=33，
    即他应缴获费33元．

    点评 本题考查了一次函数的应用，解此题的关键是能根据题意列出函数式，难度适中．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

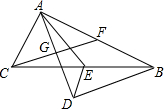    18．如图，Rt△ABC中，∠BAC=90°，点E是BC的中点，AD平分∠BAC，BD⊥AD于点D．
    （1）求证：∠ADE=∠BDE．
    （2）过点C作CG⊥AD于点G，交AB于点F，求证：DE=$\frac{1}{2}BF$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

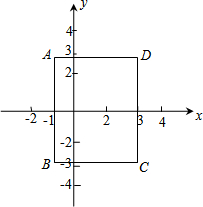    19．在平面直角坐标系中，长方形ABCD的边BC∥x轴，若A点的坐标为（-1，2$\sqrt{2}$），C点坐标为（3，-2$\sqrt{2}$）．
    （1）写出B点，D点的坐标；
    （2）若动点P沿长方形ABCD的边从A→D→C的路径运动，运动速度为$\sqrt{2}$m/s，运动时间为t（s）．
    请回答下列问题：
    ①当P点运动时间为t1=1s时，求S△BCP；
    ②当P点运动时间为t2=4s时，求S△BCP；
    ③当P在什么位置时，△BCP的面积是长方形ABCD面积的$\frac{1}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

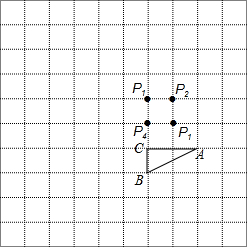    16．如图，在10×10的小正方形网格中，△ABC的顶点A、B、C在网格点上，P1、P2、P3、P4是其中一个小正方形的四个格点，将△ABC绕A点逆时针旋转90°，再向下平移2个单位，得到△A′B′C′；将△ABC按一定的规律顺次旋转，第一次将△ABC绕点P1逆时针旋转90°得到△A1B1C1；第二次将△A1B1C1绕点P2逆时针旋转90°得到△A2B2C2；第三次将△A2B2C2绕点P3逆时针旋转90°得到△A3B3C3，依次按旋转中心为P1、P2、P3、P4、P1、P2…旋转下去．
    （1）在网格中画出△A′B′C′和△A2B2C2；
    （2）△ABC至少旋转第5次后所得的三角形刚好与△A′B′C′重合．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图（1），正方形被划分为16个全等三角形，将其中若干个三角形涂黑，且满足下列条件：
    （1）涂黑部分的面积是原正方形面积的一半；
    （2）涂黑部分成轴对称图形． 如图（2）是一种涂法，请在图（4）-（6）中分别设计另外三种涂法．[在所设计的图案中，若涂黑部分全等，则认为是同一种涂法，如图（2）与图（3）]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．在平面直角坐标系中，点O为坐标原点，点A的坐标为（1，0）．将线段OA绕点O逆时针旋转∠α，当60°≤∠α≤90°，点A的纵坐标y的取值范围是$\frac{\sqrt{3}}{2}≤y≤1$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图1，直线a，b所成的角跑到画板外面去了，你有什么办法量出这两条直线所成的角的度数？
    （1）①请帮小明在图2的画板内画出你的测量方案图（简要说明画法过程）；
    ②说出该画法依据的定理．
    （2）小明在此基础上进行了更深入的探究，
    ①在图3的画板内，作出“直线a、b所成的跑到画板外面去的角”的平分线c（已知这条线平分线经过点M）．请你帮小明完成上面操作过程．（所有的线不能画到画板外，只能画在画板内）
    ②若直线a、b与画板的边直线l所成的钝角分别为130°、100°，试求①中所画的直线c与l所成的钝角．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

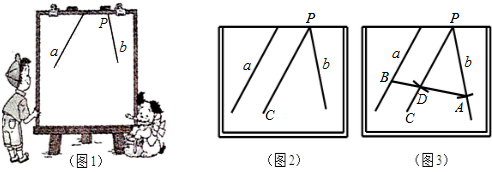
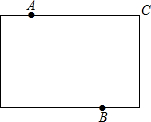    17．某地拟在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉P到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示．请利用尺规作图作出音乐喷泉P的位置．（要求：不写作法，但要保留作图痕迹，必须用铅笔作图）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

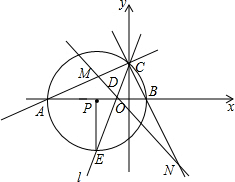    18．在平面直角坐标系中△ABC的边AB在x轴上，且OA＞OB，以AB为直径的⊙P过点C，若C的坐标为（0，2），AB=5，经过A、B、C三点的抛物线为y=ax2+bx+c．
    （1）求点A、B的坐标及抛物线的解析式．
    （2）若∠ACB的平分线所在的直线l交x轴于点D，交圆于点E．
    ①求证：PE⊥x轴；
    ②试求直线l对应的一次函数的解析式．
    （3）过点D任作一直线l分别交射线CA，CB（点C除外）于点M，N，则$\frac{1}{CM}$+$\frac{1}{CN}$的值是否为定值？若是，求出定值；若不是，请说明理由．

    查看答案和解析>>

    同步练习册答案