
分析 分别计算出将线段OA绕点O逆时针旋转∠α,当∠α=60°时,点A的纵坐标的值,当∠α=90°时,点A的纵坐标的值,即可求出范围.
解答 解:如图,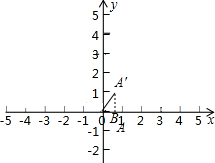
将线段OA绕点O逆时针旋转∠α,当∠α=60°时,线段OA旋转到OA′的位置,
过点A′作A′B⊥x轴于点B,
∠BOA′=60°,OA=OA′=1,
BA′=OA′•sin60°=$1×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}$,
∴此时点A′的纵坐标为$\frac{\sqrt{3}}{2}$,
将线段OA绕点O逆时针旋转∠α,当∠α=90°时,线段OA旋转到y轴上,
∴此时点A的纵坐标为1,
∴将线段OA绕点O逆时针旋转∠α,当60°≤∠α≤90°,点A的纵坐标y的取值范围是$\frac{\sqrt{3}}{2}≤y≤1$.
故答案为:$\frac{\sqrt{3}}{2}≤y≤1$.
点评 本题考查了坐标与图形变化,解决本题的关键是明确旋转后点的位置.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
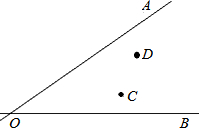 如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)
如图所示,107国道OA和320国道OB在某巿相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
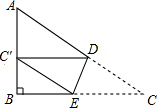 如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边的C′处,并且C′D∥BC,则CD的长是$\frac{40}{9}$.
如图,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边的C′处,并且C′D∥BC,则CD的长是$\frac{40}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
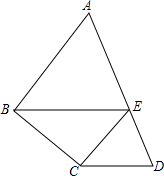 如图,在四边形ABCD中,E是AD边上的一点,EC∥AB,EB∥DC.
如图,在四边形ABCD中,E是AD边上的一点,EC∥AB,EB∥DC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
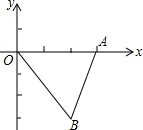 如图,平面直角坐标系中,点A、B的坐标分别为(3,0),(2,-3)若△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(-1,0),则B′点的坐标为( )
如图,平面直角坐标系中,点A、B的坐标分别为(3,0),(2,-3)若△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(-1,0),则B′点的坐标为( )| A. | ($\frac{5}{3}$,-4) | B. | ($\frac{4}{3}$,-4) | C. | ($\frac{5}{3}$,4) | D. | ($\frac{4}{3}$,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com