
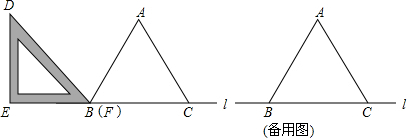
���� ��1�����õȱ������ε����ʺ͵���ֱ�������ε����ʼ��ɽ�������
��2����DF��AB�ཻ��G����G��GH��BC��H���ɵȱ������ε����ʺ͵���ֱ�������ε����ʵõ�BF��GH�ij��ȣ����������ε������ʽ�з��̿ռ���ý��ۣ�
��� 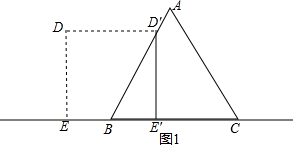 �⣺��1������D�˶���AB��ʱ����ͼ1��
�⣺��1������D�˶���AB��ʱ����ͼ1��
���ı���DEE��D���Ǿ��Σ�
��DD��=EE�䣬D��E��=DE=12��
�ߡ�ABC�ǵȱ������Σ�
���ABC=60�㣬
��BE��=4$\sqrt{3}$��
��EE��=12+4$\sqrt{3}$��
��t=4+$\frac{4\sqrt{3}}{3}$��
����D�˶���AB��ʱ��ͬ���ɵ�t=9-$\frac{4\sqrt{3}}{3}$��
�൱4+$\frac{4\sqrt{3}}{3}$��t��9-$\frac{4\sqrt{3}}{3}$ʱ�����dz�DEF�Ķ���D���ڡ�ABC�ڲ���
�ʴ�Ϊ��4+$\frac{4\sqrt{3}}{3}$��t��9-$\frac{4\sqrt{3}}{3}$��
��2����0��t��4��
��ͼ2����DF��AB�ཻ��G����G��GH��BC��H��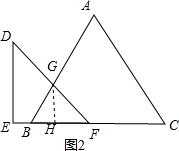
�ߡ�ABC=60�㣬��DFE=45�㣬
��BH=a����GH=HF=$\sqrt{3}$a����$\sqrt{3}+1$��a=3t��
��GH=$\sqrt{3}$a=$\frac{9-3\sqrt{3}}{2}$t��
��S=$\frac{1}{2}$BF•GH=$\frac{27-9\sqrt{3}}{4}$t2��
��4��t��5��
�ɢٵ�S��BGF=$\frac{27-9\sqrt{3}}{2}$t2��
��BE=3t-12��EH=$\sqrt{3}$��3t-12����
��S=$\frac{27-9\sqrt{3}}{4}$t2-$\frac{\sqrt{3}}{2}$��3t-12��2=$\frac{27-27\sqrt{3}}{4}$t2+36$\sqrt{3}t$-72$\sqrt{3}$��
���� ���⿼���˵ȱ������ε����ʣ�����ֱ�������ε����ʣ��������⣬�����ε�����������������ʣ���ȷ�Ļ���ͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
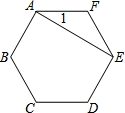 ��ͼ������������ABCDEF�У�����AE����tan��1=$\frac{\sqrt{3}}{3}$��
��ͼ������������ABCDEF�У�����AE����tan��1=$\frac{\sqrt{3}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
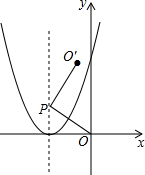 ��ͼ����ƽ��ֱ������ϵ�У���P��������y=x2+4x+4�Գ����ϵ�����һ�㣬���߶�OP�Ƶ�P��ʱ�뷽����ת90��õ��߶�PO�䣮����O�������������ϣ����P�������ǣ�-2��2����-2��-1����
��ͼ����ƽ��ֱ������ϵ�У���P��������y=x2+4x+4�Գ����ϵ�����һ�㣬���߶�OP�Ƶ�P��ʱ�뷽����ת90��õ��߶�PO�䣮����O�������������ϣ����P�������ǣ�-2��2����-2��-1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
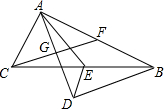 ��ͼ��Rt��ABC�У���BAC=90�㣬��E��BC���е㣬ADƽ�֡�BAC��BD��AD�ڵ�D��
��ͼ��Rt��ABC�У���BAC=90�㣬��E��BC���е㣬ADƽ�֡�BAC��BD��AD�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ס���������A��ʻ��B�أ��׳����ҳ�����ʻ2h��������;����Ϣ��0.5h����Ϣǰ���ٶ���ͬ����ͼ�Ǽ���������ʻ�ľ���y��km����ʱ��x��h���ĺ���ͼ��
�ס���������A��ʻ��B�أ��׳����ҳ�����ʻ2h��������;����Ϣ��0.5h����Ϣǰ���ٶ���ͬ����ͼ�Ǽ���������ʻ�ľ���y��km����ʱ��x��h���ĺ���ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | 900 | 920 | 950 | 1010 | 1050 | 1100 |
| ���� | 1 | 1 | 2 | 3 | 1 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com