Question

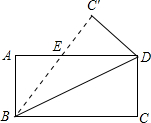
18．如图，将长方形纸片ABCD沿对角线BD折叠，使点C落在C′处，BC′交AD于E．若∠DBC=22.5°，则在不添加任何辅助线的情况下，图中45°的角（虚线也视为角的边）有（　　）

• A． 3个
• B． 4个
• C． 5个
• D． 6个

Answer 1

分析 根据折叠可得△BCD≌△BC′D，进而可得∠C′BD=∠CBD=22.5°，然后可算出∠C′BC=45°，再根据矩形的性质可得AD∥BC，∠A=∠C′=∠C=90°，然后可得∠AEB=45°，∠ABE=45°，∠EDC′=45°，∠C′ED=45°，从而可得答案．

解答 解：根据折叠可得△BCD≌△BC′D，
∴∠C′BD=∠CBD=22.5°，
∴∠C′BC=45°，
∵四边形ABCD是矩形，
∴AD∥BC，∠A=∠C′=∠C=90°，
∴∠AEB=∠EBC=45°，
∴∠C′ED=45°，
∵∠A=∠C′=∠C=90°，
∴∠ABE=45°，∠EDC′=45°，
∴图中45°的角有5个．
故选：C．

点评 此题主要考查了翻折变换的性质以及矩形的性质，关键是掌握折叠后图形的大小不发生改变．