练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．从多边形的一个顶点出发引对角线，可以把这个多边形分割成7个三角形，则该多边形为九边形．

    分析 从一个n边形的某个顶点出发，可以引（n-3）条对角线，把n边形分为（n-2）的三角形

    解答 解：由题意可知，n-2=7，
    解得n=9．
    则这个多边形的边数为9，多边形为九边形．
    故答案为：九

    点评 此题主要考查了多边形，关键是掌握从一个n边形的某个顶点出发，可以把n边形分为（n-2）个三角形

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

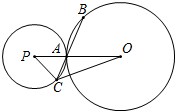    7．如图，已知⊙O的半径为5，⊙P与⊙O外切于点A，经过点A的直线与⊙O、⊙P分别交于点B、C，tan∠OAB=$\frac{\sqrt{21}}{2}$．
    （1）求AB的长；
    （2）当∠OCA=∠OPC时，求⊙P的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．设a为无理数，n为整数，我们定义：当|n-a|＜|n+1-a|时，称a靠近n．例如：因为|1-$\sqrt{2}$|＜|2-$\sqrt{2}$|，|1-$\sqrt{3}$|＞|2-$\sqrt{3}$|，$\sqrt{2}$靠近1，$\sqrt{3}$靠近2．利用计算器探究：
    （1）在$\sqrt{5}$，$\sqrt{6}$，$\sqrt{7}$，$\sqrt{8}$中哪些靠近2？哪些靠近3？
    （2）在$\sqrt{10}$，$\sqrt{11}$，$\sqrt{12}$，$\sqrt{13}$，$\sqrt{14}$，$\sqrt{15}$中哪些靠近3？哪些靠近4？
    （3）在$\sqrt{17}$，$\sqrt{18}$，$\sqrt{19}$，$\sqrt{20}$，$\sqrt{21}$，$\sqrt{22}$，$\sqrt{23}$中哪些靠近4？哪些靠近5？
    （4）猜测：在$\sqrt{{n}^{2}+1}$，$\sqrt{{n}^{2}+2}$，$\sqrt{{n}^{2}+3}$，…，$\sqrt{（n+1）^{2}-1}$共有多少个无理数？其中多少个靠近n？（友情提示：$\sqrt{（n+1）^{2}-1}$=$\sqrt{{n}^{2}+2n}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．某机械租赁公司有同一型号的机械设备40套，经过一段时间的经营发现，当每套设备的月租金为270元时，恰好全部租出，在此基础上，当每套设备的月租金每提高10元时，这种设备减少租出一套，且没租出的一套设备每月需支出费用（维护费、管理费等）20元，设每套设备的月租金为x（元），租赁公司出租该型号设备的月收益（收益=租金收入-支出费用）为y（元）
    （1）用含x的代数式表示未出租的设备数（套）以及所有未出租设备（套）的支出费用；
    （2）当月租金分别为300元和350元时，租赁公司的月收益分别是多少元？此时应该出租多少套机械设备？请你简要说明理由；
    （3）当x为何值时，租赁公司出租该型号设备的月收益最大？最大月收益为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

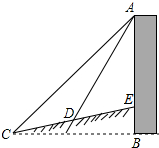    12．重庆建筑多因地制宜、依山而建，现有以住宅楼如图所示，该楼背后为一斜坡，坡角为15°，为测得该楼的高度，一兴趣小组的同学在C点测得楼顶A点的仰角为45°，点D点测的仰角为60°，CD两点之间的距离是20米，C、B在同一水平地面上，CD与AB交于点E．
    （1）求D点距离地面的垂直距离；
    （2）求斜坡最高点E点到楼顶A点之间的距离．
    （结果保留根号，参考数据：tan15°=0.27，sin15°=0.26，cos15°=0.97，$\sqrt{3}$=1.732，$\sqrt{2}$=1.414，$\sqrt{6}$=2.449）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．如图，AB∥CD，BD平分∠ABC，若∠DCB=100°，则∠D的度数是（　　）
    A．40°B．50°C．30°D．45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．|1-$\sqrt{2}$|的相反数为（　　）
    A．1-$\sqrt{2}$B．$\sqrt{2}$-1C．1+$\sqrt{2}$D．-1-$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．有一列数a1，a2，a3，…，an．其中a1=-1，a2=$\frac{1}{1{-a}_{1}}$，a3=$\frac{1}{1{-a}_{2}}$，…，an=$\frac{1}{1{-a}_{n-1}}$，则a1+a2+a3+…+a2015=1006．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知：抛物线y=-x2+bx+c经过点A（1，0），C（0，-3）
    （1）求抛物线的表达式及顶点D的坐标；
    （2）如图①，点P是直线BC上方抛物线上一动点，过点P作y轴平行线，交直线BC于点E，是否存在一点P，使线段PE的长最大？若存在，求出PE长的最大值；若不存在，请说明理由；
    （3）如图②，过点A作y轴的平行线，交直线BC于点F，连接DA、DB．四边形OAFC沿射线CB方向运动，速度为每秒1个单位长度，运动时间为t秒，当点C与点B重合时立即停止运动，设运动过程中四边形OAFC与四边形ADBF重叠部分面积为S，请求出S与t的函数关系式．

    查看答案和解析>>

    同步练习册答案