
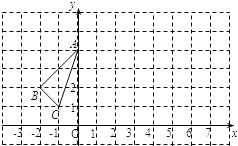
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某条直线对称?若是,请在图上画出这条对称轴.
【答案】作图见解析.
【解析】
试题分析:(1)根据轴对称图形的性质,找出A、B、C的对称点A1、B1、C1,画出图形即可;
(2)根据平移的性质,△ABC向右平移6个单位,A、B、C三点的横坐标加6,纵坐标不变;
(3)根据轴对称图形的性质和顶点坐标,可得其对称轴是l:x=3;
试题解析:(1)由图知,A(0,4),B(-2,2),C(-1,1),
∴点A、B、C关于y轴对称的对称点为A1(0,4)、B1(2,2)、C1(1,1),
连接A1B1,A1C1,B1C1,得△A1B1C1;
(2)∵△ABC向右平移6个单位,
∴A、B、C三点的横坐标加6,纵坐标不变,
作出△A2B2C2,A2(6,4),B2(4,2),C2(5,1);
(3)△A1B1C1和△A2B2C2是轴对称图形,对称轴为图中直线l:x=3.


科目:初中数学 来源: 题型:
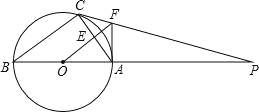
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC,交AC于点E,交PC于点F,连接AF.
(1)求证:AF是⊙O的切线;
(2)已知⊙O的半径为4,AF=3,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题的个数有( )
①如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
②过直线外一点有且只有一条直线与这条直线平行.
③两条直线被第三条直线所截,同旁内角互补.
④内错角相等,两直线平行.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a>0)的顶点为(2,4),若点(﹣2,m),(3,n)在抛物线上,则m_____n(填“>”、“=”或“<”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算:①x2+x4=x6 ②2x+3y=5xy ③x6÷x3=x3 ④(x3)2=x6,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
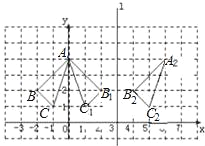
【题目】在边长为1的小正方形组成的网格中,把一个点先沿水平方向平移丨a丨格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方向平移丨b|格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得到一个新的点,我们把这个过程记为(a,b)例如在图1中.从A到B记为:A→B(+1,+3)从c到D记为:C→D(+3,一3),请回答下列问题:
(1)如图1,若点A的运动路线为:A→B→D→A,请计算点A运动过的总路程;
(2)若点A运动的路线依次为:A→M(+2,+3)A→N(+1,―1),N→P
(-2,+2)P→Q(+4,—4)请你依次在图2上标出点M,N,P,Q的位置.
(3)在图2中,若点A经过(m,n)得到点E,点E再经过(p、,q)后得到Q,则m与p满足的数量关系是___________;n与q满足的数量关系是________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com