
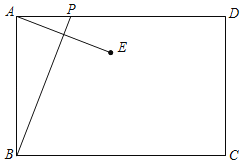
【题目】如图,已知矩形ABCD中,AB=4,动点P从点A出发,沿AD方向以每秒1个单位的速度运动,连接BP,作点A关于直线BP的对称点E,设点P的运动时间为t(s).
(1)若AD=6,P仅在边AD运动,求当P,E,C三点在同一直线上时对应的t的值.
(2)在动点P在射线AD上运动的过程中,求使点E到直线BC的距离等于3时对应的t的值.
【答案】(1)t=(6﹣2![]() )s时,P、E、C共线;(2)
)s时,P、E、C共线;(2)![]() 或4
或4![]() .
.
【解析】
(1)设AP=t,则PD=6﹣t,由点A、E关于直线BP对称,得出∠APB=∠BPE,由平行线的性质得出∠APB=∠PBC,得出∠BPC=∠PBC,在Rt△CDP中,由勾股定理得出方程,解方程即可得出结果;
(2)①当点E在BC的上方,点E到BC的距离为3,作EM⊥BC于M,延长ME交AD于N,连接PE、BE,则EM=3,EN=1,BE=AB=4,四边形ABMN是矩形,AN=BM=![]() ,证出△BME∽△ENP,得出
,证出△BME∽△ENP,得出![]() ,求出NP=
,求出NP=![]() ,即可得出结果;
,即可得出结果;
②当点E在BC的下方,点E到BC的距离为3,作EH⊥AB的延长线于H,则BH=3,BE=AB=4,AH=AB+BH=7,HE=![]() ,证得△AHE∽△PAB,得出
,证得△AHE∽△PAB,得出![]() ,即可得出结果.
,即可得出结果.
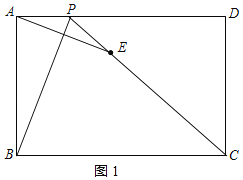
解:(1)设AP=t,则PD=6﹣t,如图1所示:
∵点A、E关于直线BP对称,
∴∠APB=∠BPE,
∵AD∥BC,
∴∠APB=∠PBC,
∵P、E、C共线,
∴∠BPC=∠PBC,
∴CP=BC=AD=6,
在Rt△CDP中,CD2+DP2=PC2,
即:42+(6﹣t)2=62,
解得:t=6﹣![]() 或6+
或6+![]() (不合题意舍去),
(不合题意舍去),
∴t=(6﹣![]() )s时,P、E、C共线;
)s时,P、E、C共线;
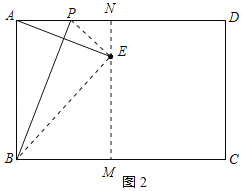
(2)①当点E在BC的上方,点E到BC的距离为3,作EM⊥BC于M,延长ME交AD于N,连接PE、BE,如图2所示:
则EM=3,EN=1,BE=AB=4,四边形ABMN是矩形,
在Rt△EBM中,AN=BM=![]() ,
,
∵点A、E关于直线BP对称,
∴∠PEB=∠PAB=90°,
∵∠ENP=∠EMB=∠PEB=90°,
∴∠PEN=∠EBM,
∴△BME∽△ENP,
∴![]() ,即
,即![]() ,
,
∴NP=![]() ,
,
∴t=AP=AN﹣NP=![]() ;
;
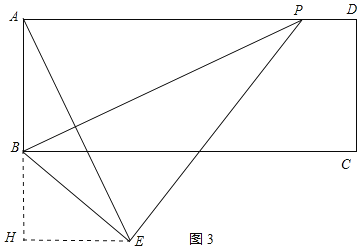
②当点E在BC的下方,点E到BC的距离为3,作EH⊥AB的延长线于H,如图3所示:
则BH=3,BE=AB=4,AH=AB+BH=7,
在Rt△BHE中,HE=![]() ,
,
∵∠PAB=∠BHE=90°,AE⊥BP,
∴∠APB+∠EAP=∠HAE+∠EAP=90°,
∴∠HAE=∠APB,
∴△AHE∽△PAB,
∴![]() ,即
,即![]() ,
,
解得:t=AP=![]() ,
,
综上所述,t=![]() 或
或![]() .
.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】在△PQN中,若∠P=![]() ∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
(1)已知△ABC是等边三角形,判断△ABC是否为“差角三角形”,并说明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判断△ABC是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
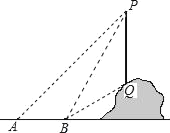
【题目】 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示的是一种折叠门,已知门框的宽度AD=2米,两扇门的大小相同(即AB=CD),且AB+CD=AD,现将右边的门CDD1C1绕门轴DD1向外面旋转67°(如图2).
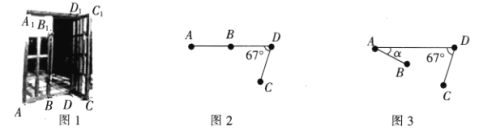
(1)求点C到AD的距离.
(2)将左边的门ABB1A1绕门轴AA1向外面旋转,设旋转角为α(如图3),问α为多少时,点B,C之间的距离最短?(参考数据:sin67°≈0.92,cos67°≈0.39,tan29.6°≈0.57,tan19.6°≈0.36,sin29.6°≈0.49)
查看答案和解析>>
科目:初中数学 来源: 题型:
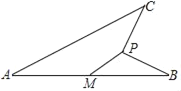
【题目】如图,线段AB=4,M为AB的中点,动点P到点M的距离是1,连接PB,线段PB绕点P逆时针旋转90°得到线段PC,连接AC,则线段AC长度的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的解析式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.在Rt△ABC中,∠ACB=90°,AC=6,BC=8.点D是BC边上一点,连接AD,若△ABD是准互余三角形,则BD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳池每次换水前后水的体积基本保持不变,当该游泳池以每小时300立方米的速度放水时,经3小时能将池内的水放完.设放水的速度为x立方米/时,将池内的水放完需y小时.已知该游泳池每小时的最大放水速度为350立方米
(1)求y关于x的函数表达式.
(2)若该游泳池将放水速度控制在每小时200立方米至250立方米(含200立方米和250立方米),求放水时间y的范围.
(3)该游泳池能否在2.5小时内将池内的水放完?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com