
【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
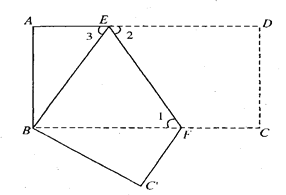
(1)折叠后,DC的对应线段是 ,CF的对应线段是 ;
(2)若∠1=50°,求∠2、∠3的度数;
(3)若CD=4,AD=6,求CF的长度.
【答案】(1)BC′,FC′ (2) ∠2=50°,∠3=80°(3)CF=![]()
【解析】试题分析: (1)根据折叠的性质即可得出;
(2)∠2=∠BEF.由AD∥BC得∠1=∠2,所以∠2=∠BEF=50°,从而得∠3=80°;
(3)设CF=x,在△BC′F中根据勾股定理即可求出.
试题解析:
(1)由折叠的性质可得:折叠后,DC的对应线段是BC′,CF的对应线段是C′F;
(2)由折叠的性质可得:∠2=∠BEF,
∵AD∥BC,
∴∠1=∠2=50°.
∴∠2=∠BEF=50°,
∴∠3=180°50°50°=80°;
(3)∵CD=4,AD=6,
∴设CF=x,则BF=6-x,
根据勾股定理得![]() ,
,
即![]() ,
,
解得x=![]() .
.
∴CF=![]() .
.


科目:初中数学 来源: 题型:
【题目】小文,小亮从学校出发到青少年宫参加书法比赛,小文步行一时间后,小亮骑自行车沿相同路线行走,两人均匀速前行,他们的路程差s(米)与小文出发时间t(分)之间的关系如图所示. 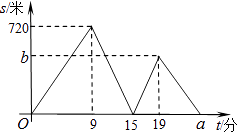
(1)求小文和小亮的速度各是多少?
(2)求学校到少年宫的距离.
(3)求图中的a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣23+(π﹣3.14)0﹣(1﹣2 ![]() )×(﹣
)×(﹣ ![]() )﹣1
)﹣1
(2)5a2b÷(﹣ ![]() ab)(2ab2)2
ab)(2ab2)2
(3)(2x﹣y)(2x+y)﹣(x﹣3y)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)发现:
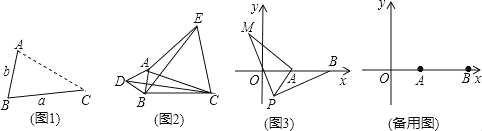
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.
(1)求证:△AOE≌△COF;
(2)若EF⊥AC,试判断四边形AFCE是什么特殊四边形?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
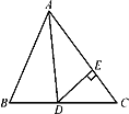
【题目】如图所示,在△ABC中,已知AD是角平分线,∠B=66°,∠C=54°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com