

 ,BP=6,AP=
,BP=6,AP= ,求QC的长.
,求QC的长. .
. ,可计算出BC=
,可计算出BC= ,在Rt△BPQ中,利用余弦的定义得cosB=
,在Rt△BPQ中,利用余弦的定义得cosB= ,可计算出BQ=10,然后利用QC=BQ-BC进行计算即可.
,可计算出BQ=10,然后利用QC=BQ-BC进行计算即可. ,
,  ,
, .
. ,
,
 .
. ,
, .
.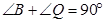 .
. .
.  ,
,
 是⊙
是⊙ 的半径,
的半径, 是⊙
是⊙ 的切线.
的切线. ,
, 中,
中, ,
, ,
, 是⊙
是⊙ 的直径,
的直径, .
. 中,
中, .
. .
.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com